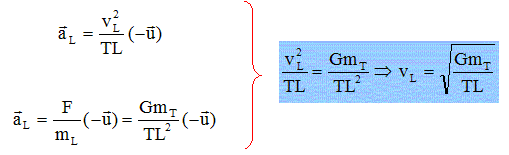Gravitation : système Terre - Lune, concours ingénieur Geipi 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

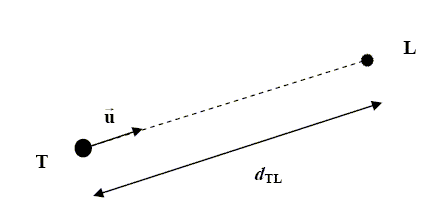
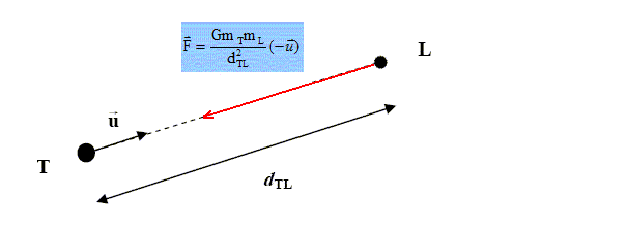
On se propose d'étudier le mouvement de la Lune autour de la Terre. Dans ce cadre, seul le système Terre-Lune en interaction seule est considéré. L'influence des autres astres n'est donc pas prise en compte. La Terre et la Lune sont assimilées à deux points matériels T et L de masses respectives mT et mL. La distance entre ces deux points est notée dTL. On note ur le vecteur unitaire porté par la droite passant par les deux points T et L (voir figure ). On ne tient pas compte de la rotation de la Terre sur elle même et on néglige tous les frottements. Enfin, on note G la constante de l'attraction universelle. mT = 5,980 1024 kg mL = 8,1 1022 kg RT = 6370 km RL =1723 km dTL= 387200 km G = 6,67 10-11 SI Calculer la distance TC entre le centre de la Terre T et le centre d'inertie C du système Terre-Lune. mT TC = mL LC avec dTL = TC+ LC mT TC = mL (dTL-TC) ; TC = mL dTL / (mT + mL). TC = 8,1 1022 *387 200 / (5,980 1024 +8,1 1022) =5,17 103 km. Quelle est la nature exacte de la trajectoire de la Lune autour de la Terre ? Trajectoire elliptique. Dans la suite du problème, on admet pour simplifier les calculs, que le mouvement de la Lune autour de la Terre est circulaire uniforme.     Quelle est la nature de la force F qui s'exerce sur la Lune ? Force de gravitation attractive exercée par la terre. Placer cette force sur le schéma. Donner l’expression et calculer son intensité F. F = 6,67 10-11*5,980 1024*8,1 1022 / (3,872 108)2 =2,15 1020 N. Quelle est l'unité de la constante de l'attraction universelle ? G = F d2/( mL mT) ; d est une distance ; [d2]=L2 ; mL et mT sont des masses [mL mT] = M2. F: force soit masse * accélération soit masse * longueur / temps2 ; [F]=M L T-2. [G]=L2M-2 M L T-2; [G]=L3 M-1 T-2.   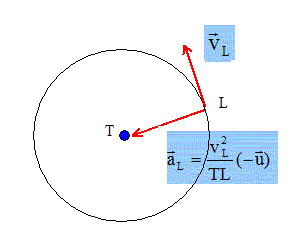Donner l'expression vectorielle du vecteur accélération de la Lune. En appliquant le principe fondamental de la dynamique, donner une seconde expression pour ce même vecteur accélération. Tracer sur le schéma la vitesse la Lune. Exprimer puis calculer son module vL. vL = [6,67 10-11*5,980 1024 / 3,872 108 ]½ =1014,95 =1,015 103 m/s. Quelle est la période de rotation T de la lune autour de la Terre. Donner sa valeur en jours (J), heures (h), minutes (mn) et secondes (s). La lune décrit une circonférence 2pdLT en ne période T, à la vitesse vL : 2pdLT = vL T soit T = 2pdLT / vL. T = 6,28 * 3,872 108 / 1,014,95 103 =2,396 106 s = 27 J 17 h 50 min 14 s.

retour -menu