Circuit inductif, concours ingénieur Geipi 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

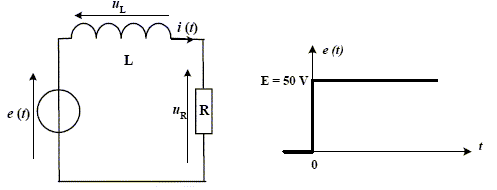
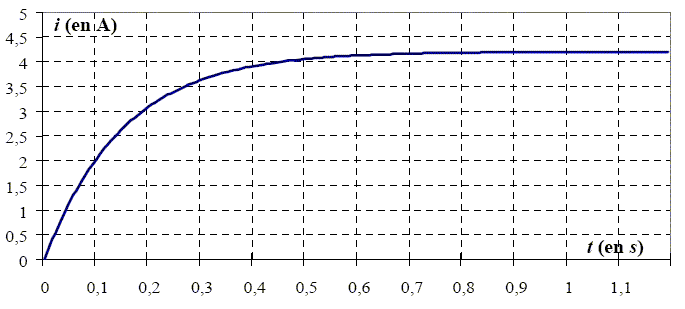
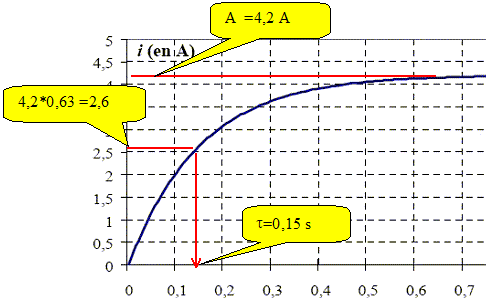
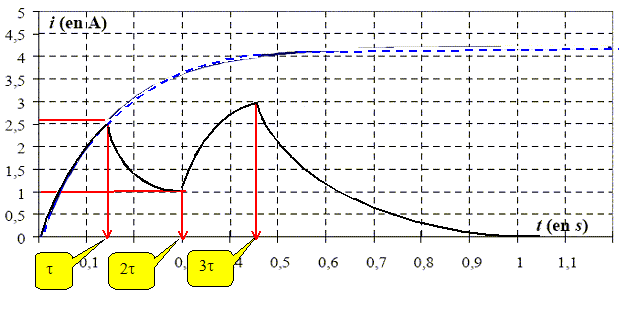
Dans le problème suivant, on veut étudier l’action d’une inductance sur la forme de l’intensité. Ecrire l'équation différentielle de variable i (t) caractérisant le circuit ci-dessus. additivité des tensions : e(t) = Ldi/dt + Ri di/dt + R/L i = e(t)/L. (1) L'équation donnant l'intensité durant la charge est : i (t) = A + B exp (-t /t) (2) Donner les expressions de A, B et t en fonction de E, R et L. di/dt = -B/t exp (-t /t), repport dans (1) : -B/t exp (-t /t) +R/L A + R/L B exp (-t /t)= e(t)/L B (R/L-1/t) exp (-t /t) +R/L A = e(t)/L Egalité vérifiée quel que soit t si t = L/R ; A = e(t)/R. A t=0, l'intensité i est nulle ; (2) donne A+B=0 soit B= -A ; B= -e(t)/R. i (t) = e(t)/R [1- exp (-t /t)]. A partir de l'enregistrement i (t) ci-dessous, trouver les valeurs de A, B et t. En déduire R et L.   0,15 = L/R ; 4,2 = E/R soit R = E/4,2 = 50 /4,2 ; R=12 W. L = 0,15 R = 0,15*12 ; L=1,8 H.   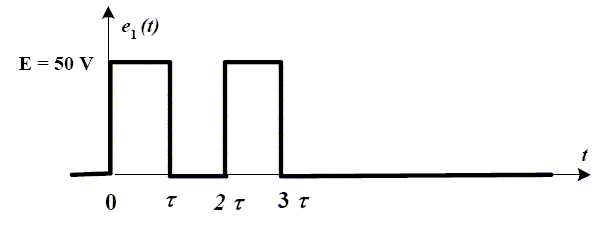On remplace la tension e (t) par la tension e1 (t). Tracer l'allure de l'évolution de i (t) entre 0 et 1 s. On considère l'évolution de i (t) pour 0 < t < t. Calculer la valeur de i ( t). i (t) = 4,2 [1- exp (-t /t)] ; i(t) = 4,2 (1-exp(-1)) = 2,65 ~2,6A. On considère maintenant l'évolution de i (t) pour t < t > 2t . On pose t' = t - t. L'équation donnant l'intensité durant la décharge est : i (t') = A' + B' exp (-t'/ t ). Déterminer A' et B'. En déduire la valeur de i (t = 2t). Continuité de l'intensité à t=t ( ou à t'=0) : i(0) = 2,6 = A'+B'. En fin de décharge i=0 d'où : A'=0 et par suite B' = 2,65 A. i(t') = 2,65 exp (-t'/ t ). i(t) = 2,65 exp(-1) = 1,0 A. On considère maintenant l'évolution de i (t) pour 2t < t < 3 t. Calculer la valeur de i (t =3t). On pose t'' = t - 2t. L'équation donnant l'intensité durant la nouvelle charge est : i(t") = A"+B" exp (-t''/ t ). Si le régime permanent pouvait être atteint i = 4,2 =A" Continuité de l'intensité à t = 2t ( ou t"=0 ) : 1 = A"+B" ; par suite B" = 1-A"=1-4,2 =-3,2 A i(t") = 4,2 -3,2exp (-t''/ t ). i(3t) = i (t"=t) = 4,2 -3,2 exp(-0,1)= 3,0 A.

retour -menu