lentilles : étude d'un compte-fils concours technicien finances 05 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

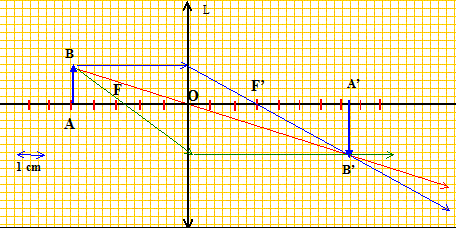
Le compte-fils permet la visualisation de la trame d'un tissu. Il est constitué d'une simple lentille convergente. Deux utilisations possibles d'une lentille convergente sont étudiées ci-dessous. Dans tout l'exercice, on prendra AB comme objet et A'B' son image par la lentille de centre optique 0 et de foyers F et F'. L'objet AB mesure 0,5 mm et A est sur l’axe. Premier cas : L'objet à visualiser est placé en avant de F, à 5 cm de la lentille. Construisez l'image A'B'. La distance focale est de 3 cm.   Les distances algébriques sont écrites en gras et en bleu. Indiquez quelles sont les valeurs algébriques : OA, OA', AB, A'B'. OA = -0,05 m ( 0,05 m à gauche de la lentille) AB = 5 10-4 m ; OF' = 0,03 m Formule de conjugaison des lentilles minces : 1/OF' = 1/OA'-1/OA ; 1/OA'=1/OF' +1/OA 1/OA'= 1/0,03+1/(-0,05) =(0,05-0,03) / (0,03*0,05) =2/0,15 OA'= 0,15/2 = 0,075m = 7,5 cm. Grandissement transversal : g = OA' / OA = 7,5 / (-5) = -1,5. g =A'B' / AB d'où A'B' = -1,5AB = -1,5*0,5 = -0,75 mm. Précisez la nature de l'objet AB et la nature de son image A'B’. L'objet est réel : situé à gauche de la lentille. L'objet est à l'intersection des rayons incidents. L'image est réelle: située à droite de la lentille. L'image est à l'intersection des rayons émergents. Comparez la taille de l'objet et de son image. L'image est renversée par rapport à l'objet : sa taille est égale à 1,5 fois celle de l'objet.   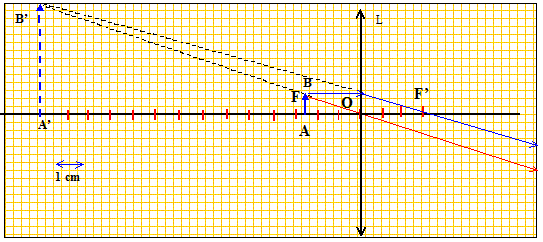Web www.chimix.com Deuxième cas : L'objet est placé entre F et O. Un objet droit AB mesurant 0,5 mm, ayant A sur l'axe optique, est situé à 2,5 cm de la lentille convergente. La distance focale de celle-ci est de 3 cm. Donnez les valeurs de OA, OF', et AB. OA = -0,025 m ; OF' = 0,03 m ; AB = 5 10-4 m. En utilisant les formules des lentilles : Calculez OA'. Formule de conjugaison des lentilles minces : 1/OF' = 1/OA'-1/OA ; 1/OA'=1/OF' +1/OA 1/OA'= 1/0,03+1/(-0,025) =(0,025-0,03) / (0,03*0,025) =-6,67 OA'= -1/6,67 =-0,15 m = -15 cm. Indiquez la nature de l'image. L'image est virtuelle : située à gauche de la lentille L'image est à l'intersection du prolongement des rayons émergents. L'image est droite, même sens que l'objet. Donnez la taille en mm de l'image A'B'. g = OA' / OA =-15 / (-2,5) = 6. g =A'B' / AB d'où A'B' = 6AB = 6*0,5 = 3 mm. Conclusion: Des deux cas étudiés ci-dessus, indiquez celui qui correspond à la modélisation d'un compte-fils. Justifiez votre réponse. Le deuxième cas correspond au fonctionnement en loupe : L'image est 6 fois plus grande que l'objet ; l'image est droite, virtuelle, et peut être observée par l'oeil.

retour -menu