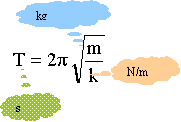Dipôle RC, effet Doppler, oscillateur élastique concours EPF 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

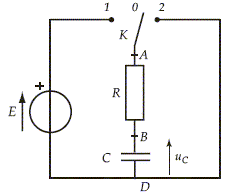
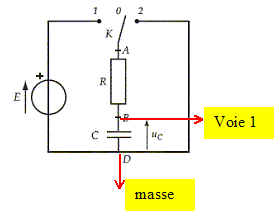
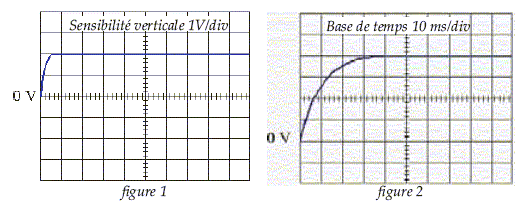
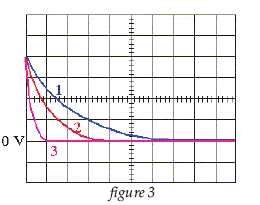
Dipôle RC. Un élève étudie les phénomènes de charge et décharge d'un condensateur de capacité C =1 mF à travers un conducteur ohmique de résistance R. La charge se fait sous une tension constante E. Le condensateur est supposé parfait. L'élève réalise le montage schématisé ci-dessus : Etablir l'équation différentielle donnant les variations de la tension uC en fonction du temps lorsque l'interrupteur est en position 1. La loi d'additivité des tensions appliquée aux bornes du dipôle RC permet d'écrire: uR+uC=E La loi d'Ohm appliquée au dipôle ohmique permet d'écrire: uR=R i. or i = dq/ dt = q' ( dérivée de la charge par rapport au temps) mais q=CuC => q' =CduC/dt et uR=RCduC/dt. Finalement l'équation différentielle cherchée s'écrit: RCduC/dt+uC=E. On suppose la fonction du temps uC(t) = A(1-exp(-t/t)) solution de l'équation différentielle établie précédemment. Montrer que A = E et établir l'expression littérale de t . duC/dt =A/t exp(-t/t); repport dans l'équation différentielle : RC A/t exp(-t/t) + A(1-exp(-t/t)) = E (RC A/t-A) exp(-t/t) +A = E. On identifie A à E et RC A/t-A à zéro d'où t = RC. Quelle est la valeur de uC en régime permanent ? Le terme contenant l'exponentielle tend vers zéro et uC tend vers E en régime permanent. Quel est le nom donné à la constante t ? Déterminer l'unité de cette constante. t : constante de temps. R : énergie joule = RI2t d'où R = Ej /(I2t) R a la dimension d'une énergie divisée par un temps et par une intensité au carrée.   C : énergie stockée par le condensateur : EC = ½Q2/ C avec Q = It d'où C =0,5I2t2/EC. C a la dimension d'une intensité au carré multipliée par un temps au carré et divisé par une énergie. Par suite RC a la dimension d'un temps.     Recopier sur votre copie le circuit étudié et indiquer les branchements à effectuer sur l’oscilloscope pour observer l’évolution de la tension uC. L’interrupteur étant placé en position 1, on obtient l’oscillogramme de la figure 1. Afin de mieux exploiter son enregistrement, l’élève modifie les réglages de l’oscilloscope et obtient la courbe représentée par la figure 2. Quelle est la sensibilité verticale, après que l'élève ait affiné ses réglages ? 0,5 V / div. D'autres réglages ont-ils été modifiés ? Si oui, lesquels ? Décalage vertical de deux divisions vers le bas. La sensibilité horizontale ( base de temps ) a été diminuée. Déterminer graphiquement la valeur de la constante t . Au bout d'une durée égale à 5 t le régime permanent est atteint : 5 t~ 4*10 = 40 ms t~ 8 ms = 8 10-3 s. En déduire la valeur de la résistance R. R = t /C = 8 10-3/10-6 = 8000 W. L'élève bascule ensuite l'interrupteur K et observe ainsi la décharge du condensateur. Les réglages étant dans les mêmes que dans le cas de la figure 2, indiquer parmi les trois courbes proposées à la figure 3 celle qui correspond à la décharge du condensateur. Justifier.   La constante de temps est identique à la décharge et à la charge ; les réglages étant inchangés par rapport à la figure 2, la courbe 2 convient.   analyse de l'effet Doppler. Une source S, qui émet des " bips " à la période T se d�éplace à vitesse constante vs vers un observateur fixe situé en O. Le bip se propage à la célérité c dans l'air. A l'instant initial (t = 0), la source (distante de d1 du point O) émet son premier bip. A quel instant t1 l'observateur reçoit-il le premier bip ? t1 = d1/c. La source émet, tout en se déplaçant, des bips régulièrement avec une période T. A quelle distance d2 de l'observateur se trouve la source lorsqu'elle émet son deuxième bip ? d2 = vsT. A quel instant t2 (compté depuis l'émission de premier bip) l'observateur reçoit-il son deuxième bip ? t2 =T+ d2/c = T +vs/cT. Trouver une relation entre la période T' des bips reçus par l'observateur et la période T des bips émis pas la source. T' = t2-t1 = T (1-vs/c). Déterminer ensuite la relation entre la fréquence ƒ' et la fréquence ƒ émise ? La fréquence est l'inverse de la période : f' = (c-vs ) / c f. Le spectre de la lumière des galaxies lointaines est décalé vers le rouge et ce décalage augmente avec la distance des galaxies au système solaire. Peut-on appliquer à la lumière l'étude précédente ? Si oui, donner une explication à ce phénomène. L'effet Dopler s'applique à la lumière. Les fréquences des radiations rouges sont plus petites que celles de la lumière visible.  Or f' = (1-vs/c) f conduit à f' <f , décalage vers des fréquences plus faibles. 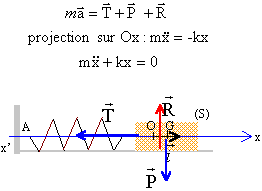Oscillateur élastique. Dans ce sujet on étudie le mouvement d’un solide S de masse m attaché à un ressort de constante de raideur k. Le solide se déplace horizontalement et les frottements sont négligés. A l’instant de date t = 0 s, on écarte horizontalement le solide de sa position d’équilibre d’une distance x0 et on l’abandonne sans vitesse initiale. Faire un schéma du dispositif masse-ressort. Etablir l’´équation différentielle du mouvement du centre d’inertie G du solide. Référentiel galiléen : la Terre ; système étudié : le solide de masse m. Le solide est soumis à 3 forces : P :action gravitationnelle de la Terre sur le solide (poids du solide). R action normale de la piste sur le solide.on néglige les frottements. T: tension, action du ressort sur le solide. Déduire l’expression de la période propre T0 en fonction de k et m. On mesure 15 oscillations en t = 15, 6 s. Calculer T0. période T : pulsation w0 (rad/s )telle que w0²= k/m T0 = 15,6 / 15 =1,04 s.   Le solide S est surchargé par un autre solide S1 de masse m1, fixé sur S. Ce nouveau système est excité et l’on mesure 15 oscillations en t = 16, 05 s. Déterminer l’expression de la période T1 associée à l’ensemble en fonction de k, m1 et m. Dans l'expression précédente de la période, il suffit de remplacer m par m+m1. T1 = 2p [(m+m1) / k]½ ; T1 = 16,05/15 =1,07 s. A l’aide des questions précédentes, montrer que l’on peut écrire K sous la forme : k = Am1 / (T12-T02) ; m = BT02 avec A et B deux constantes à préciser. T02 =4p2 m / k soit m = k T02/ (4p2) T12 =4p2 (m+m1)/k ; k T12 / (4p2) = m+m1 = k T02/ (4p2) + m1. k / (4p2) [ T12 -T02 ] = m1 ; k = 4p2 m1 / [ T12 -T02 ]. On identifie : A = 4p2. m = k T02/ (4p2) ; on identifie B = k/4p2. Déterminer la valeur de la constante de raideur k du ressort et celle de la masse m du solide S. m1 = 20 g. k = 4*3,142*0,020 / (1,072-1,042) = 12,47 N/m. m = 12,47/(4*3,142) * 1,042 = 1,08 kg.

retour -menu