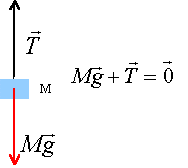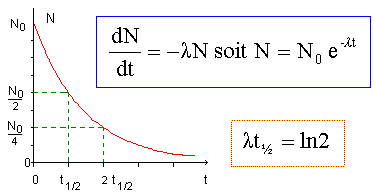Détermination de la constante de raideur d'un ressort, désintégration du plutonium 238 . Concours manipulateur électroradiologie médicale Corbeil 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

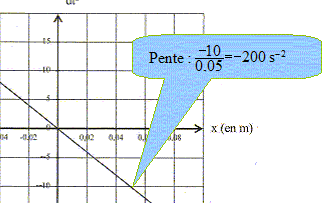
Constante de raideur d'un ressort. Partie A : Un ressort, supposé sans masse, de longueur à vide L0 est accroché par une extrtémité à une potence. A l'autre extrémité est suspendu un solide de masse m. L'ensemble est vertical et la longueur est alors L. Faire le schéma de la situation. Faire le bilan des forces s'appliquant au solide S dans le référentiel terrestre.   Enoncer en justifiant la relation traduisant l'équilibre de S dans le référentiel du laboratoire et exprimer k en fonction de m, g, L et L0. La masse fixée au ressort étant pseudo-isolée, tension et poids sont opposées ( principe d'inertie). Ces forces ont la même valeur. mg = k(L-L0). En déduire la valeur numérique de k. m = 100 g ; L0 = 400 mm ; L= 449 mm ; g = 9,8 N/kg. k = mg / (L-L0) = 0,1*9,8 /( 0,449-0,400 ) = 20 N m-1.   Partie B. 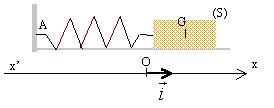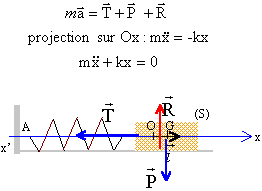Le ressort et le solide sont placés sur un banc à coussin d'air horizontal. L'extrémité libre est accrochée à un point fixe et les frottements seront considérés comme négligeables. Au repos, G, centre d'inertie de S est en O, pris comme origine des abscisses sur l'axe horizontal Ox.   On écarte G de sa position d'équilibre suivant Ox et on lâche S. Un système informatisé permet d'obtenir le graphe suivant : Faire un iventaire des forces s'exerçant sur S dans une position quelconque de G au cours de son mouvement dans le référentiel terrestre. R : action du plan opposée au poids P ; T : force de rappel exercée par le ressort. Montrer que l'équation différentielle du mouvement s'écrit : d2x/dt2 = -k/m x. x est l'abscisse de G. Ecrire la seconde loi de Newton suivant l'axe Ox : -kx = md2x/dt2 soit d2x/dt2 = x" = -k/m x. En expliquant la méthode utilisée et à l'aide du graphe ci-dessus, déterminer la valeur de k. ( m = 0,1 kg) Le graphe est une fonction linéaire décroissante de pente ( coefficient directeur) -k/m = -k/0,1 = -10 k. Par suite -10 k = -200 soit k = 20 N m-1. Cette valeur est identique à celle trouvée ci-dessus. Vérifier que la fonction x(t) = Xm cos (w0t+j) est solution de l'équation différentielle ; déterminer l'expression de w0 et la période T0 puis la calculer. x'=dx/dt = -Xmw0 sin (w0t+j) ; x" = -Xmw20 cos (w0t+j) Repport dans l'équation différentielle : -Xmw20 cos (w0t+j) =-k/m Xmcos (w0t+j) On identifie : w20 = k/m ; w0 = (k/m)½. Or T0 = 2p/ w0 = 2p (m/k)½. T0 = 6,28 ( 0,1/20)½ =0,44 s.   Désintégration du plutonium 238. La désintégration du plutonium 238 23894Pu produit un noyau d'uranium 234 23492U. Ecrire l'équation de désintégration en précisant les lois utilisées. De quel type de radioactivité s'agit-il ? 23894Pu --> 23492U + AZX Conservation de la charge : 94=92+Z soit Z=2. Conservation du nombre de nucléons : 238 = 234+A soit A = 4. 23894Pu --> 23492U + 42He. Emission d'un noyau d'hélium , : radioactivité de type alpha. Le temps de demi-vie du plutonium 238 est 87,8 ans. Définir le temps de demi-vie et donner la relation entre le temps demi-vie t½ et la constante radioactive l. Durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés ; durée au bout de laquelle l'activité initiale est divisée par deux. lt½ = ln2. Compléter le graphique donnant l'évolution de l'activité en fonction du temps. Quelle est l'énergie libérée, en Joule, lors de la désintégration d'un noyau de plutonium 238 ? Données : m( 23894Pu) = 3,952073 10-25 kg ; m(23492U) = 3,885528 10-25 kg m(42He) = 6,644691 10-27 kg ; c = 2,9979 108 m/s. |Dm|= |m(42He) + m(23492U) -m( 23894Pu)| = 3,952073 10-25 - 3,885528 10-25- 6,644691 10-27 |Dm|=9,809 10-30 kg. E = |Dm| c2 = 9,809 10-30 *(2,9979 108)2 =8,8157 10-13 J. La puissance que doit développer la pile est P= 56,0 mW Quelle énergie doit fournir la pile par seconde ? Energie (J) = puissance (W) * durée (s) E = 0,056*1 = 0,056 J. Montrer qu'il faut 6,35 1010 désintégrations par seconde pour fournir cette énergie. Une désintégration fourni 8,8157 10-13 J d'où 0,056/8,8157 10-13 = 6,35 1010 désintégrations par seconde. L'activité de la source est A=6,35 1010 Bq. Que devient cette activité au bout de 10 ans. De quel pourcentage a t-elle baissée ? Ecrire la loi de décroissance radioactive : A = A0 exp(-lt). ln (A0 /A) = lt avec lt ½ = ln2 d'où : ln (A0 /A) = ln2 t/t½. ln (A0 /A) = ln2 * 10 / 87,8 = 7,89 10-2 ; A0 /A = 1,082 ; A = A0 /1,082 =6,35 1010/1,082 A = 5,87 1010 Bq. (6,35-5,87)/6,35*100 =7,6 % de baisse.  Quelle masse de plutonium est nécessaire pour fournir une activité de 6,35 1010 Bq ? M(Pu) = 238 g/mol et NA = 6,02 1023 mol-1 ; l = 2,50 10-10 s-1. A = l N ; A : activité en Bq ; l: constante radioactive en s-1 ; N : nombre de noyaux présents à la date t. N= A/l = 6,35 1010 / 2,50 10-10 = 2,54 1020 noyaux n=N/ NA = 2,54 1020 /6,02 1023 = 4,22 10-4 mol. m = n M = 4,22 10-4 *238 =0,10 g.

retour -menu