Lentille et miroir plan concours kiné Ceerrf 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

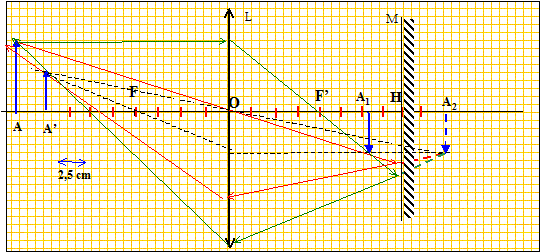
L'objectif d'un appareil photographique est assimilé à une lentille mince convergente L de distance focale image f' = 10,0 cm. L'image se forme sur une plaque rectangulaire, centrée sur l'axe optique, de dimensions l' x L' = 24 mm x 36 mm. La mise au point est faite avec un objet à l'infini, ce qui correspond à une position A1 pour la plaque sur l'axe. Que vaut OA1. Justifier. L'image d'un objet situé à l'infini se forme dans le plan focal image de la lentille. OA1 = OF' = 10,0 cm. On veut maintenant photographier un objet situé à 50,0 cm devant l'objectif . Exprimer puis calculer la position de l'image A2. Les distances algébriques sont écrites en gras et en bleu. Formule de conjugaison : 1/f' = 1/OA2 - 1/OA. 1/OA2 = 1/OA + 1/f' ; OA2 = OA f' / (f'+OA) avec OA = -0,5 m et f'=0,1 m. OA2 = -0,5*0,1 / (0,1-0,5) = 0,05 / 0,4 = 0,5/4 = 12,5 cm. En déduire le déplacement d= A1A2. OA2 = OA1+A1A2 ; A1A2 = OA2 - OA1. A1A2 =12,5-10,0 = 2,50 cm. Il faut éloigner la plaque de la lentille .   Techniquement , la mise au point ne permet pas d'éloigner la plaque de plus de 5,0 cm de A1. Exprimer puis calculer la distance minimale d'un objet, par rapport à l'objectif, pour réaliser une photographie nette. OA2 = OA1+0,05 = f'+d Repport dans la formule de conjugaison : 1/f' = 1/OA2 - 1/OA. 1/OA = 1/OA2 - 1/f' = 1/(f'+d)-1/f' ; OA = -[f' (f'+d)/ d = -0,10*0,15/0,05 = -0,30 m. L'objet étant à la distance minimale , exprimer puis calculer les dimensions l et L du plan photographié. Grandissement transversal |g| = OA2 / |OA |=15/30 = 0,5. La taille de l'objet est égale à deux fois la taille de l'image : l= 2 l' = 48 mm ; L = 2L' = 72 mm.   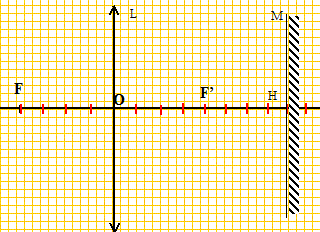On utilise la même lentille L mais avec un nouveau dispositif ; on place un miroir plan M à 20,0 cm derrière L, perpendiculaire à l'axe optique. Le sens positif choisi est celui de la propagation de la lumière. On note A : point objet de l'axe optique ; A1 image de A donnée par L ; A2 image de A1 donnée par M ; A' image de A2 donnée par L. Ecrire OH en fonction de f'. OH = 2 f'. Exprimer OA1 en fonction de f' et OA. formule de conjugaison : 1/f' = 1/OA1 - 1/OA ; 1/OA1 =1/f'+1/OA. OA1 = OA f' / (OA +f' ) Exprimer OA2 en fonction de f' et OA. A1 H =A1 O +OH =OH-OA1 =2f'-OA1. A2 est le symétrique de A1 par rapport au plan du miroir et la lumière change de sens après réflexion : A1 H =HA2. H A2 = OA2 - OH = OA2-2f' ; OA2 = H A2+2f' = A1H+2f'. OA2 = A1 O +4f' ; OA2 = -OA f' / (OA +f' )+ 4f'. Exprimer OA' en fonction de f' et OA2. A2 sert d'objet réel pour la lentille ; la lumière après réflexion se déplace vers la gauche. OA' >0 ; OA2<0. L'image définitive A' est réelle. formule de conjugaison : 1/f' = 1/OA' - 1/OA2 ; 1/OA' =1/f'+1/OA2. On choisit un sens positif contraire au précédent. Reécrire OA' en fonction de f' et OA2. La formule de conjugaison s'écrit : -1/f' = -1/OA'+ 1/OA2 ; 1/OA' =1/f'+1/OA2. En déduire OA' en fonction de f' et OA. OA2 = -OA f' / (OA +f' )+ 4f'. Calculer OA' si OA = -10,0 cm. Conclure. A confondu avec F : l'image A1 se trouve à l'infini ; il en est de même de A2. A' se trouve alors en F, confondue avec l'objet A.

retour -menu