Oscillateur élastique constitué de deux ressorts verticaux concours kiné Ceerrf 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

Dans le référentiel terrestre supposé galiléen, on considère R1 et R2 deux ressorts à spires non jointives, disposés suivant la verticale IJ, et de constantes de raideur respectives k1 et k2. Les ressorts sont reliés par une masse ponctuelle et leurs extrémités I et J sont fixes. On note l1 et l2 les longueurs respectives de R1 et R2. l01 et l02 sont les longueurs à vide. On note D=IJ. Le pendule ainsi constitué peut osciller dans un plan vertical sans frottement. Etude statique. 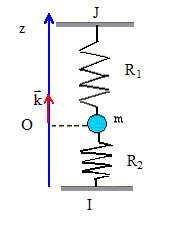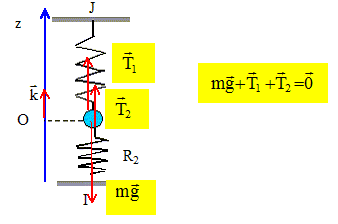A l'équilibre, la cote de la masse m coincîde avec l'origine de l'axe. Les grandeurs vectorielles sont écrites en gras et en bleu. La masse est au repos. Ecrire les tensions T1 et T2 des deux ressorts. R1 étiré a tendance à être rappelé vers sa position à vide : (l1-l01) >0 et T1 dirigée vers le haut. R2comprimé a tendance à être rappelé vers sa position à vide : (l2-l02) <0 et T2 dirigée vers le haut. T1 = k1(l1-l01) k ; T2 = k2(l02-l2)k. Ecrire la condition vectorielle d'équilibre.   En déduire une expression de la masse m : k1(l1 éq-l01) + k2(l02-l2 éq) = mg ; m = [ k1(l1 éq-l01) + k2(l02-l2 éq)] / g. (1) Etude dynamique. à t = 0 on écarte m de sa position d'équilibre et on la lâche sans vitesse initiale. Etablir l'expression de l'équation différentielle du mouvement de m. On note z la position de la masse m au dessus de O : l1 = l1 éq-z ; l2 = l2 éq+z. La seconde loi de Newton s'écrit suivant l'axe (O, z) : k1(l1-l01) + k2(l02-l2) - mg = mz" k1( l1 éq-z -l01) + k2(l02- l2 éq-z) - mg = mz" k1(l1 éq-l01) -k1z + k2(l02-l2 éq)- k2 z -mg = mz" et en tenant compte de (1) : -k1z - k2 z = mz". z" + (k1+k2)/m z = 0. (2)   La fonction z(t) = Zm cos ( 2pf0t+j) est solution de cette équation différentielle. Nommer et donner les unités des constantes Zm , f0 , j . Zm : amplitude en mètre ; f0 : fréquence en Hertz ; j : phase à l'origine en radian. Déterminer l'expression de f0. w02 = (k1+k2)/m ; w0 = 2p f0 ; f0 = 1/( 2p ) [(k1+k2)/m]½. Les conditions initiales sont : vz(0)=0 ; z(0) = Z0 avec Z0 <0. Exprimer la loi horaire du mouvement en fonction de Z0, k1, k2, m. z(0) = Zm cos j = Z0. L'amplitude Zm étant positive, Zm = | Z0| et cos j =-1 ; j =p. z(t) = | Z0| cos ( [(k1+k2)/m]½ t+p). Exprimer la loi horaire du mouvement en fonction de Z0, k1, k2, m mais avec une fonction sinus. cos ( a+p) = sin (a-½p) z(t) = | Z0| sin ( [(k1+k2)/m]½ t-½p). 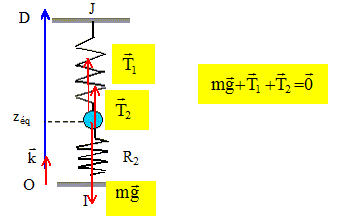Nouveau repère. L'origine de l'axe est le point I. Refaire le schéma en indiquant sur l'axe zéq la côte de la masse à l'équilibre et D. A partir de la condition vectorielle d'équilibre, déterminer une expression de la masse m, notamment en fonction de zéq et D. k1(l1 éq-l01) + k2(l02-l2 éq) = mg. l2 éq= zéq ; l1 éq=D-zéq ; k1(D-zéq-l01) + k2(l02-zéq) = mg. k1(D-l01) + k2 l02 - zéq(k1+ k2) =mg m = [k1(D-l01) + k2 l02 - zéq(k1+ k2) ] /g.

retour -menu