Condensateur, bobine inductive, générateurs de tension et de courant concours kiné Ceerrf 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

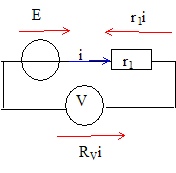
Condensateur. On considère un condensateur initialement déchargé ( C inconnue), deux conducteurs ohmiques identiques ( résistance R), et un générateur de tension ( E=30 V, r1= 10 W). Pour mesurer la tension à vide ( f.e.m) de ce générateur on branche un voltmètre à ces bornes. Expliquer à l'aide d'un calcul, pourquoi on mesure bien la tension à vide ( f.e.m ), la résistance du voltmètre notée RV étant très grande. 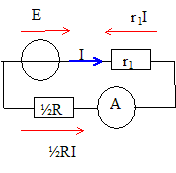Additivité des tensions : E = RVi + r1 i ; i = E/(RV + r1 ) Tension mesurée par le voltmètre U = RVi = RV E/(RV + r1 ) = E/ (1+ r1 /RV). Si RV >> r1 alors U= E. On associe les deux conducteurs ohmiques en parallèle et on les relie au générateur. Un ampèremètre branché dans le circuit mesure une intensité I=500 mA. Exprimer I en fonction des données. Les deux conducteurs ohmiques identiques, montés en parallèle se comporte comme un conducteur ohmique unique de résistance ½R.    Additivité des tensions : E= r1I+½RI ; I = E/(r1+½R). En déduire l'expression littérale et la valeur de R. R= 2(E/I- r1). R= 2*(30/0,5-10) =100 W.   On charge le condensateur avec un autre générateur ( même tension à vide E1 mais résistance interne négligeable) en série avec le premier conducteur ohmique. On le décharge ensuite dans le second conducteur ohmique. Rappeler sans démonstration l'expression de : la tension uC aux bornes du condensateur en charge : uC= E1(1-exp(-t/(RC)). la tension uD de ce même condensateur lors de sa décharge ( on considère que la nouvelle origine des temps se situe au début de cette décharge) : uD= E1exp(-t/(RC)). la constante t du circuit de charge : t = RC. Lors de la charge, le condensateur atteint 63 % de sa charge à t=0,20 ms. En déduire l'expression littérale puis la valeur de C ( mF). C= t /R avec t= t = 0,20 ms = 2 10-4 s ; R= 100 W. C = 2 10-4/100 =2 10-6 = 2mF.   On reprend le même condensateur initialement déchargé. On le charge avec un générateur idéal de courant, délivrant un courant d'intensité constante I=11 mA. On relève la tension, notée u, aux bornes du condensateur en fonction du temps. La représentation graphique de cette tension est modélisable sous la forme u(t) = 5,0 t ( unités S.I). Etablir l'expression de u(t). Charge du condensateur q(t) = Cu(t). de plus, l'intensité étant constante, q(t) = I t d'où u(t) = I/C t. Montrer qu'elle est compatible avec la modélisation proposée. En déduire la valeur de C. I/C est une constante ; u(t) est proportionnelle au temps. L'expression u(t) = I/C t est compatible avec u(t) = 5,0 t. On identifie I/C = 5,0 avec I= 1,1 10-5 A. C = I/5 = 1,1 10-5 /5 = 2,2 10-6 F = 2,2 mF. On considère que deux mesures sont en accord si l'écart relatif entre elles est inférieur à 10 %. Est-ce le cas entre les valeurs trouvées ci-dessus ? différence des deux valeurs / moyenne des deux valeurs * 100 = (2,2 -2)/2,1*100 = 9,5 %. 9,5% < 10 % : les valeurs sont donc en accord. On suppose que la relation u(t) = 5,0 t est fiable. On arrête la charge du condensateur à t = 10 s. On souhaite alors l'utiliser pour alimenter un petit moteur électrique capable de monter une charge m = 50 g d'une hauteur h= 5,5 cm. L'opération est-elle réalisable ? ( g = 10 N/kg.  Tension aux bornes du condensateur à t = 10 s : U = 5*10 = 50 V. Energie stockée dans le condensateur : Ec=½CU2 = 0,5 * 2 10-6 *502 = 2500 10-6 = 2,5 10-3 J. Energie mécanique lors de la montée de la charge : Em=mgh = 5 10-2*10*5,5 10-2 =27,5 10-3 J. Em >> Ec, l'opération n'est pas réalisable. 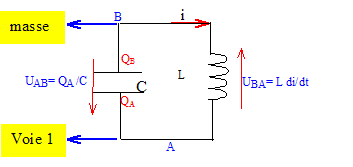Bobine inductive. Le condensateur précédent ( initialement déchargé) est chargé à l'aide d'un générateur idéal de tension ( E= 10 V). Il est ensuite isolé. On note A et B les armatures du condensateur. A porte une charge positive. A t=0, on le relie à une bobine inductive idéale d'inductance L=0,20 H. On prendra la capacité du condensateur trouvée à la première question. On pose uC ( tension aux bornes du condensateur) = uAB. Représenter le circuit en indiquant les connexions d'un oscilloscope permettant de visualiser la tension uC. Quel phénomène physique observe t-on ? Oscillations libres non amorties ( oscillateur électrique LC) Etablir l'équation différentielle à laquelle obéit uC(t). uAB+uBA=0 ; uC + Ldi/dt = 0 ; or i = dq/dt = CduC/dt ; di/dt = Cd2uC/dt2. par suite : uC + L Cd2uC/dt2=0 ; d2uC/dt2 + 1/(LC) uC =0. On considère que la solution de cette équation différentielle est du type uC(t) = A cos ( at+B) où A, a et B sont des constantes. Déterminer les expressions de A, a et B en fonction de E, L et C. duC/dt = -Aa sin (at+B) ; d2uC/dt2= -Aa2 cos (at+B) Repport dans l'équation différentielle : A cos ( at+B) -Aa2 /(LC)cos (at+B) =0 Acos ( at+B) (1-a2 /(LC)) = 0 d'où a = (LC)-½. à t=0, le condensateur est chargé uC=E = A cos B avec A positif ; d'où A= E et B=0. Exprimer puis calculer la période propre T0 du phénomène. Prendre p~3; 10-0,5 ~ 0,3. T0 = 2p/a = 2p (LC)½ = 2*3 (0,2*2 10-6)½ =6 (0,4 10-6)½ = 6 10-3*0,4½ =6 10-3*(4 10-1)½ =12 10-3*0,3 =3,6 10-3 s. Rappeler sans démonstration l'expression de l'énergie électromagnétique d'un circuit LC en régime libre. Retrouver l'équation différentielle du circuit précédent. EL= ½Li2 ; EC= ½CuC2. l'énergie du dipôle LC reste constante d'où : ½Li2 + ½CuC2 = Cte. Dériver par rapport au temps : L i di/dt + C uC duC/dt = 0 or i = dq/dt = CduC/dt ; di/dt = Cd2uC/dt2. d'où : LCduC/dt Cd2uC/dt2 + CuC duC/dt = 0 Après simplification : LCd2uC/dt2 +uC= 0. On considère maintenant que la bobine n'est pas idéale et possède une résistance interne r. A partir de la question précédente, établir la nouvelle équation différentielle à laquelle obéit uC(t). Lors des échanges d'énergies entre condensateur et bobine, l'énergie du dipôle diminue de la valeur ri2t ( effet joule) Pendant l'intervalle de temps dt, très petit, l'énergie du condensateur varie de la valeur d(½q2/C) et l'énergie magnétique de la bobine varie de d(½Li2) ; l'énergie perdue par effet joule est ri2dt. Bilan énergétique : d(½q2/C) + d(½Li2) + ri2dt =0. d(½q2/C)/dt + d(½Li2) /dt+ ri2 =0. 1/C q dq/dt + L i di/dt + ri2 =0 ; or i = dq/dt ;di/dt = d2q/dt2. 1/C q i + Li d2q/dt2 + ri2 =0 ; 1/C q + Ld2q/dt2 + ri =0 ; 1/C q + Ld2q/dt2 + rdq/dt =0 ; Or q= CuC d'où : uC +LCd2uC/dt2 + rCduC/dt=0.

retour -menu