Le téléphone pot de yaourt examen d'admission audioprothesiste Rennes 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

A l'ère du téléphone portable, il est encore possible de communiquer avec un système bien plus archaïque…   L'onde sonore produite par le premier interlocuteur fait vibrer le fond du pot de yaourt, le mouvement de va et vient de celui-ci, imperceptible à l'œil, crée une perturbation qui se propage le long du fil. Cette perturbation fait vibrer le fond du second pot de yaourt et l'énergie véhiculée par le fil peut être ainsi restituée sous la forme d'une onde sonore perceptible par un second protagoniste. 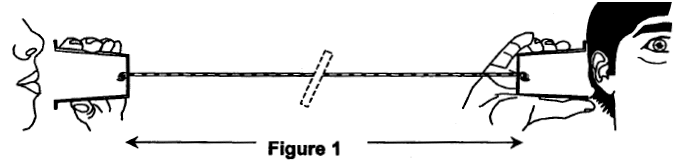Données : célérité du son dans l'air à 25°C vair = 340 m.s-1  A ) A propos des ondes : Identifier la chaîne des différents milieux de propagation des ondes mécaniques au sein du dispositif : de la bouche de la personne qui parle, à l'oreille de la personne qui écoute (figure 1). L'onde sonore se propage en premier dans l'air, ensuite dans le fond du 1er pot de yaourt, dans le fil, dans le fond du 2ème pot de yaourt et enfin dans l'air. 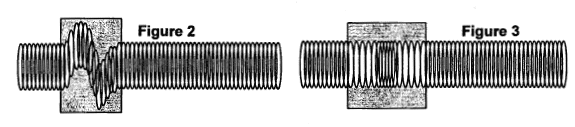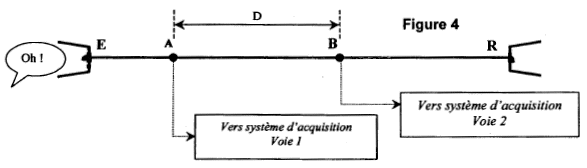Ce fil légèrement élastique peut être modélisé par un ressort à spires non jointives. Les schémas suivants illustrent les conséquences de deux modes de déformation d'un ressort : l'écartement d'une extrémité du ressort selon une direction perpendiculaire à l'axe de celui-ci produit une onde de cisaillement (figure 2), alors qu'une déformation selon l'axe du ressort produit une onde de compression (figure 3).      Attribuer, à chacune des situations représentées sur les figures 2 et 3, les termes d'onde longitudinale et d'onde transversale. Justifier votre réponse. Seul le second mode de déformation (figure 3) correspond au phénomène observé sur le fil du dispositif étudié par la suite. Figure 2 : Onde transversale, la direction de la perturbation (ici la verticale) est perpendiculaire à la direction de propagation de l'onde. (ici l'horizontale). Figure 3: Onde longitudinale, la direction de la perturbation et la direction de propagation de l'onde sont identiques. B ) Célérité de l'onde qui se propage le long du fil : A 25°C, on réalise le montage suivant (figure 4), afin de mesurer la célérité des ondes sur le fil du dispositif. Deux capteurs, reliés en deux points A et B distants de D = 20 m sur le fil, détectent successivement le passage d'une perturbation générée par un son bref à l'entrée du pot de yaourt émetteur E.   Les capteurs enregistrent l'amplitude de cette perturbation au cours du temps. A partir de l'enregistrement (figure 5), déterminer avec quel retard t, par rapport au point A, le point B est atteint par le signal. retard : 4 divisions soit 4*5 10-3 = 2 10-2 s. Donner l'expression de la célérité v de l'onde sur ce fil en fonction de D et t. Calculer sa valeur. Comparer cette valeur à celle de la célérité du son dans l'air à 25°C. Quelle propriété justifie ce résultat ?  célérité (m/s) = distance (m) / durée (s) =D/ t= 20 / 0,02 = 1000 m/s. Cette valeur est bien supérieure à la célérité du son dans l'air : une onde se propage plus rapidement dans un solide que dans un gaz. Plus le milieu est rigide, plus la célérité est grande. Le fil ER de longueur L = 50 m est assimilé à un ressort de constante de raideur k = 20 kg.s-2 et de masse linéique m = 1,0.10-3 kg.m-1 . Dans le cas d'un fil, le produit k.L est une constante caractéristique du milieu de propagation. Un modèle simple de la célérité v d'une onde de ce type dans ce fil correspond à l'une des expressions suivantes :  (1) v = ( m /(k.L))½ (2) v = ( k.L / m )½ (3) v = k.L / m Retrouver la bonne expression parmi celles proposées en effectuant une analyse dimensionnelle. [µ] = [M].[L]-1 ; [k] = [M].[T]-2 ; [k.L] = [M].[T]-2.[L] [µ] [k.L]-1= [M].[L]-1[M]-1.[T]2.[L]-1=[T]2 [L]-2 [µ]½ [k.L]-½ =[T] [L]-1 expression (1) non retenue l'expression (2) est l'inverse de l'expression (1) : l'expression (2) correspondant à une vitesse est retenue. l'expression (3) est l'expression (2) élevée au carrée, soit une vitesse au carrée. Calculer la célérité de l'onde sur le fil ER.  v= (20*50/10-3)½=1000 m/s. Une autre méthode, permettant de déterminer la célérité v de l'onde se propageant dans le fil, consiste à placer, devant le pot de yaourt émetteur, un haut parleur (figure 6) qui émet des ondes sonores sinusoïdales de fréquence fE. les ondes sinusoïdales qui se propagent dans le fil ont la même fréquence.   .  Lorsque la distance D est égale à 20,0 m, on obtient l'enregistrement de la figure 7.   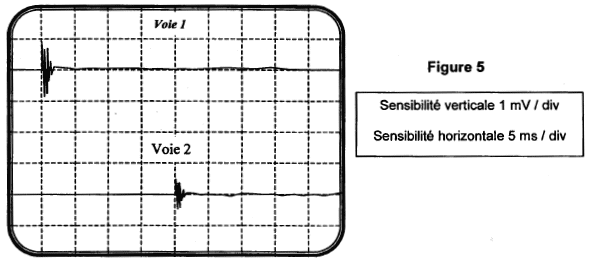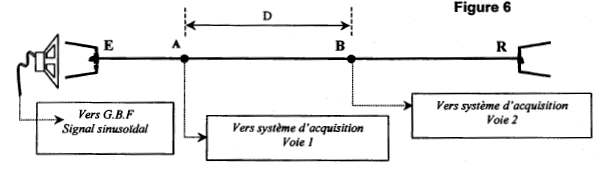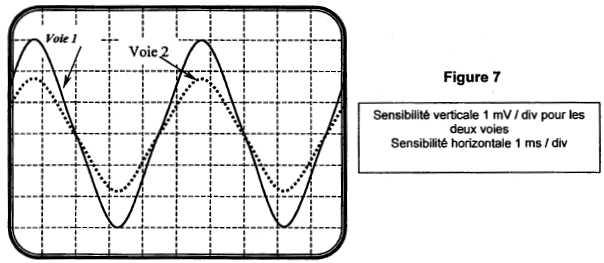Comment peut-on expliquer que l'amplitude du signal au point B (voie 2) soit plus faible que l'amplitude du signal  au point A (voie 1) ? Le point A est plus près de l'émetteur (haut-parleur) que le point B. L'onde s'amortit durant sa propagation dans le milieu. L'amplitude de la perturbation diminue lorsqu'on s'éloigne de la source (émetteur) A partir de l'enregistrement de la figure 7, déterminer la fréquence de l'onde qui se propage dans le fil. période : 5 divisions soit 5 *10-3 = 5 10-3 s fréquence f = 1/5 10-3 = 200 Hz. 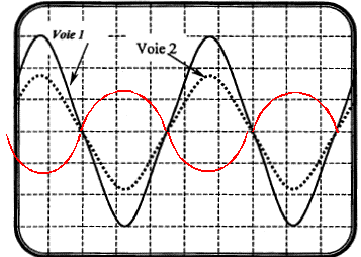Lorsque l'on éloigne le point B, du point A, on constate que les signaux se retrouvent dans la même configuration pour les valeurs de la distance : D = 25,0 m, D = 30,0 m , D = 35,0 m … En déduire la valeur de la longueur d'onde l associée à l'onde qui se propage dans le fil, puis la célérité v de cette onde. Les signaux se retrouvent dans le même état lorsque D = n.l avec n entier. en conséquence l = 5 m. célérité de l'onde : v (m/s) = l f = 5*200 = 1000 m/s. Sur la figure de l'annexe II à rendre avec la copie, représenter l'allure de la courbe que l'on observerait sur la voie 2 si la distance D était égale à 27,5 m. Si D = 27,5 m, D =(2n+1) ½l avec n = 5. Les deux signaux sont en opposition de phase à chaque instant. Le signal de la voie 2 possède une amplitude plus faible (amortissement )     La voix est un signal complexe constitué d'ondes sonores de fréquences différentes. A l'écoute des signaux transmis, le fil ne semble pas être un milieu de propagation notablement dispersif. Qu'est-ce qu'un milieu dispersif ? Quelle serait la conséquence sur les signaux reçus si le fil qui constitue le dispositif était un milieu de propagation très dispersif ? Dans un milieu dispersif, la célérité de l'onde dépend de sa fréquence. Si le fil était un milieu dispersif, les ondes de basses fréquences ( sons graves) se propageraient avec une célérité différente des ondes de hautes fréquences (sons aigus). Si le milieu était dispersif , le téléphone pot de yaourt ne pourrait pas marcher correctement. L'antenne d'un téléphone portable, émet ou reçoit des ondes électromagnétiques qui ont les mêmes propriétés que la lumière.  Quelle différence fondamentale existe-t-il concernant la propagation des ondes du téléphone "pot de yaourt" et celles d'un téléphone portable ? Les ondes électromagnétiques se propagent dans le vide contrairement aux ondes mécaniques qui nécessitent l'existence d'un milieu matériel.

retour -menu