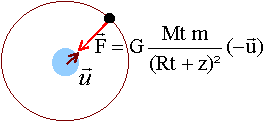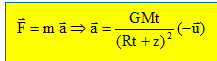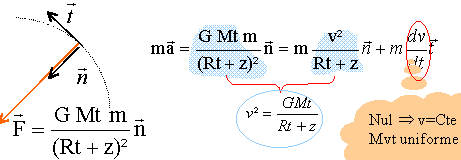Le principe du GPS : satellite, ondes, horloges examen d'admission audioprothesiste Rennes 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

Les différentes parties du problème portent sur les satellites et la mesure du temps. Elles s'appuie sur un texte paru dans la revue " La Recherche" dont les extraits sont écrits en italique. A. Les satellites. Principe : au lieu d'utiliser des repères terrestres ou de suivre les étoiles, l'utilisateur, muni d'un récepteur, mesure la distance entre lui-même et au moins 4 des 24 satellites de la constellation Navstar. Le récepteur convertit ces distances pour retrouver la latitude, la longitude et l'altitude. Répartis sur 6 orbites inclinées de 55 ° par rapport à l'équateur, ces satellites évoluent à une altitude de 20180 km. Avec une vitesse proche de 14000 km/h, ils accomplissent un tour du monde en 12 heures. Leur configuration movante a été calculée pour qu'au moins quatre d'entre eux soient toujours en vue depuis n'importe quel endroit de la planète. On rappelle que l'orbite de ces satellites est circulaire. Données : Intensité de la pesanteur au sol : g = 9,80 m s-2 ; constante de gravitation universelle : G= 6,67 10-11 N m2 kg-2. Rayon terrestre RT= 6380 km ; masse de la terre: MT = 5,98 1024 kg. Quelle est l'expression vectorielle de l'accélération d'un satellite en fonction des données ? z : altitude du satellite. Le satellite n'est soumis qu'à la force de gravitation centripète. Ecrire la seconde loi de Newton : Démontrer que le mouvement du satellite est uniforme. Dans le repère de Frenet :   Autre méthode : La force de gravitation étant perpendiculaire à la vitesse à chaque instant, ne travaille pas et en conséquence ne modifie pas l'énergie cinétique du satellite. La valeur de la vitesse reste donc constante : mouvement uniforme. Par contre la direction de la vitesse change et l'accélération n'est pas nulle. Quelle est l'expression de sa vitesse en gonction de G, Rt, Mt, z dans un référentiel géocentrique ? Mt : masse (kg) de la planète ; m : masse du satellite (kg) ; Rt (m) rayon planète ; z (m) altitude depuis le sol suivant l'axe n la seconde loi de Newton s'écrit : GMt m /(Rt+z)² = m a N= mv²/ (Rt+z) d'où la valeur de la vitesse (m/s): v² =GMt / (Rt+z). indépendante de la masse du satellite Vérifier que la vitesse des satellites sur leur orbite et la période T de rotation, données dans le texte, sont coimpatibles avec l'altitude. Un satellite décrit une circonférence de rayon Rt+z à la vitesse v durant une période T 2p(Rt+z) = v T. avec v = 14 000 km/h ; T = 12 h ; Rt+z en km. Rt+z = 14000*12/6,28 ~26750 km d'où z = 26750-6380 = 20370 km. Cette valeur est compatible avec celle donnée dans le texte( 20180 km), l'écart relatif étant : (20370-20180) / 20280 *100 ~ 1%. Un tel satellite est-il géostationnaire ? Justifier. Un satellite géostationnaire tourne dans le même sens que la terre, à la même vitesse angulaire dans le plan de l'équateur. Il paraît fixe pour un observateur terrestre. Les satellites utilisés pour le GPS ne sont pas géostationnaires. B Les ondes. Toutes les millisecondes, les satellites émettent des signaux codés sous forme d'onde radio émises sur deux fréquences différentes ( 1,6 et 1,2 GHz) dont la réception au sol va permettre de calculer la position. Un certain nombre de facteurs limite encore, et de façon systématique, la précision du GPS. Par exemple, puisque le signal du GPS n'est émis que toutes les millisecondes, un récepteur mobile verra chuter la précision de ces mesures d'autant plus qu'il se déplace vite. Autre difficulté nuisant à l'exactitude : les ondes ne se propagent pas à vitesse constante dans la partie la plus haute de l'atmosphère, car celle-ci n'est pas homogène. Tous ces éléments font que les récepteurs vendus aujourdh'ui dans le commerce affichent une erreur standard de l'ordre de 20 m. Les ondes radio sont des ondes électromagnétiques comme la lumière et se propagent dans le vide à la célérité c = 3,00 108 m/s. On négligera dans cette question les perturbations introduites par l'atmosphère sur la durée du trajet des ondes. Calculer les longueurs d'onde dans le vide des ondes émises par les satellites. Longueurs d'onde dans le vide des ondes émises par les satellites : l = c / f avec f : fréquence en Hz ; c, célérité en m/s, l : longueur d'onde en m. Pour f = 1,6 109 Hz : l1 = 3,00 108 / 1,6 109 =0,1875 m soit l1 = 0,19 m. Pour f = 1,2 109 Hz : l2 = 3,00 108 / 1,2 109 = 0,25 m. Quelle est la durée t mise par le signal pour aller du satellite S au récepteur R si le satellite est situé à la verticale de R à l'altitude h= 20 180 km ? t = h / c avec h : distance RS en m ; c : célérité en m/s et t: durée en s. h = 2,018 107 m ; t = 2,018 107 / 3,00 108 = 6,73 10-2 s. Pour une mesure unique, l'erreur sur la distance verticale est de 20 m en standard. Calculer (en nanosecondes) l'erreur Dt sur la durée de propagation du signal. Commenter. t = h/c ; Dt / t = Dh / h soit Dt = Dh t / h = Dh / c Dt = 20 * 6,73 10-2 / 2,018 107 = 6,7 10-8 s = 67 ns. La durée t de propagation du signal est environ 106 fois plus grande que l'erreur Dt. L'erreur sur la distance verticale sera d'autant plus petite que la mesure de t sera plus précise. . Pour une série de N mesures, les lois de la statistique montrent que l'erreur est divisée par un facteur N½. Calculer N pour que l'erreur passe de 20 m à 20 cm. 20 mètres = 100 * 20 centimètres : l'erreur doit être divisée par 100. N½=100 ; N= 104. En fait, entre le récepteur et le satellite le signal traverse les couches successives de l'atmosphère et se propage alors à une célérité différente de c. La fréquence et la longueur d'onde du signal sont-elles modifiées lors de la traversée de l'atmosphère ? Justifier. L'atmosphère est un milieu dispersif pour l'onde radio : la célérité de l'onde dépend de la fréquence. La fréquence de l'onde reste constante, tandis que la célérité et la longueur d'onde varient. Les horloges. Avant l'invention du GPS, pour connaître leur longitude, les navigateurs comparaient l'heure locale ( heure déterminée d'après la position du soleil ou d'un étoile) et au même moment l'heure du méridien de Greenwich donnée par une horloge embarquée sur le navire. La précision de la position du navire dépendait de la précision de la mesure de cet écart angulaire. Dans une horloge à balancier, pour une faible amplitude a, la période T vérifie la relation T = T0 ( 1+a2/16) avec T0 = 2p(l/g)½ où l est la longueur du balancier et g l'intensité du champ de pesanteur, a est en radian. Montrer par analyse dimensionnelle, que (l/g)½ est homogène à une durée : l est une longueur : [ l ]= L g est une accélération, soit une longueur divisée par le carré d'une durée : [g]=L T-2. [ l / g ] = T2 ; [ (l/g)½ ] = T. Quel est l'écart relatif par rapport à T0 observe-t-on sur la période de ce pendule lorsque l'amplitude est de 4° ? T = T0 ( 1+a2/16) ; DT/ T0 =(T-T0 ) /T0= a2/16 4 degrés = 4 *3,14 / 180 = 6,98 10-2 rad DT/ T0 = (6,98 10-2)2/16 = 3,0 10-4. Une horloge à balancier a une période T1 = 2,000 s en un lieu où l'accélération de la pesanteur vaut g1 = 9,810 N.kg-1. Calculer la période T2 d'une horloge identique de même longueur en un lieu où g2 = 9,800 N.kg-1 en conservant la même amplitude. T1 = 2p ( l/g1)½ ; T2 = 2p ( l/g2)½ ; T2 / T1 = ( g1 /g2)½ ; T2 = T1 ( g1 /g2)½. T2 = 2,000 ( 9,810 /9,800)½ = 2,001 s. Pourquoi une horloge à balancier ne convient-elle pas pour déterminer une longitude ? Quand le bateau change de latitude au cours de son voyage, la valeur de g change : en conséquence, une horloge à balancier ne convient pas pour déterminer une longitude. 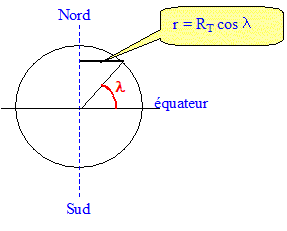En 1764, pour s'affranchir de cet inconvénient, John Harrison parvint à fabriquer une horloge utilisant un ressort spiral, qui après un voyage aller et retour entre Plymouth et La Barbade ne dériva pas de plus de 15 s en 156 jours. Calculer de la précision de l'horloge : 156 jours = 156*24*3600 secondes = 1,35 107 s. 15 / 1,35 107 = 1,1 10-6. Distance, en kilomètres, calculée sur le parallèle de Plymouth, correspondant aux 15 s de dérive observées lors du voyage de John Harrison : La latitude de Plymouth est de 50° nord. Rayon de la Terre : RT = 6380 km On rappelle que la latitude l d'un point P est l'angle entre le plan de l'équateur et la droite joignant P au centre de la Terre. Un parallèle est un cercle de rayon r à la surface de la Terre. Tous les points de ce cercle sont à la même latitude l. r = 6380 cos 50 = 4100 km. Un point situé à la surface de la Terre à la latitude de Plymouth décrit une circonférence de rayon r en 24 heures ( 86400 s) valeur de la circonférence 2pr = 2*3,14*4100 = 2,6 104 km dérive : 2,6 104 * 15 / 86400 = 4,4 km. Cette dérive est suffisamment importante pour conduire à un naufrage si la visibilité est mauvaise.

retour -menu