Mouvement d'une bille dans une goutière : énergie mécanique, base de Frenet concours kiné Assas 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

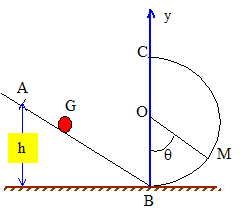
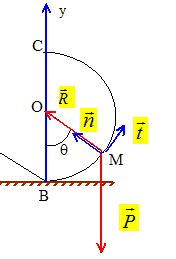
Il est demandé l'expression des valeurs littérales avant tout calcul numérique. Les notations du texte doivent être respectées. Une bille de masse m, assimilée à son centre d'inertie G, glisse sans frottement dans une gouttière inclinée puis aborde un demi-cercle de rayon r. La bille est lâchée sans vitesse d'un point A. g = 10 m/s2 ; r =OM=50 cm. Exprimer la vitesse vB de G en B. En A l'énergie mécanique de la bille est sous forme potentielle de pesanteur ; l'origine de cette énergie est prise en B, altitude zéro. EM(A) = mgh. En B, l'énergie mécanique de la bille est sous forme cinétique : EM(B) = ½mv2B. En absence de frottement, l'énergie mécanique se conserve : ½mv2B = mgh ; vB =[2gh]½. Représenter sur un schéma les forces appliquées à G au point M ainsi que les vecteurs de la base de Frenet.   Exprimer la vitese de G en M en fonction de vB et de q, puis en fonction de h et q. En B, l'énergie mécanique de la bille est sous forme cinétique : EM(B) = ½mv2B. En M, l'énergie mécanique de la bille est sous forme cinétique et potentielle de pesanteur : EM(M) = ½mv2M+mghM. hM = OM-OMcosq = r(1-cosq) En absence de frottement, l'énergie mécanique se conserve : ½mv2B = ½mv2M+mgr(1-cosq). v2M =v2B-2gr(1-cosq). Or v2B =2gh d'où : v2M =2gh-2gr(1-cosq). Exprimer la norme de R, action du support en M en fonction de h et q. Ecrire la seconde loi de newton en M suivant l'axe n de la base de Frenet. R-mg cosq = m v2M/r ; R = mg cosq + m v2M/r R = mg cosq + m(2gh/r-2g(1-cosq)) R = mg[ 2h/r -2+3cosq].   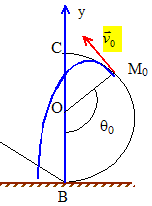On lâche la bille d'une hauteur h=2r. Exprimer la norme de R, en M, en fonction de q. R = mg[ 2h/r -2+3cosq] ; R = mg[2+3cosq]. Pour quelle valeur q0 la bille quitte t-elle le support ? Celle-ci atteint-elle le point C ? Si R devient nulle, la bille quitte le support : 2+3 cosq0 = 0 ; cosq0 =-2/3 ; q0 = 132 °. En C, l'angle q vaut 180 ° : la bille ne peut atteindre le point C. On note M0 la position de G pour q=q0. Donner l'expression de la vitesse v0 de G en M0 en fonction de r. Calculer v0. v20 =2gh-2gr(1-cosq0) avec h=2r et cosq0 =-2/3. v20 =g( 4r-2r -4r/3) ; v20 =2gr/3 ; v0 =[2gr/3 ]½ = [2*10*0,5/3]½ = 1,8 m/s. Décrire qualitativement le mouvement ultérieur de la bille. Chute libre avec vitesse initiale v0.

retour -menu