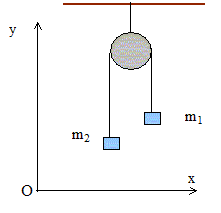Masses et poulie ; chariot sur un plan incliné concours kiné APHP 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

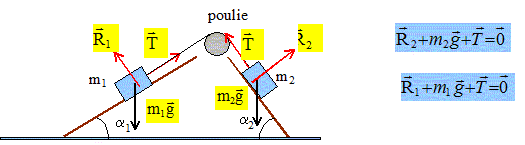
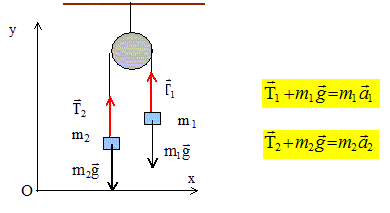
Masses et poulies. On Considère le système suivant : le fil est inextensible et de masse négligeable ; la masse de la poulie est négligeable. Les frottements sont négligés. Effectuer un bilan des forces pour chacune des masses. Chaque masse est soumise à son poids et à la tension du fil. Que peut-on dire des tensions T1 et T2 ? La masse des fils, de la poulie étant négligeable, les frottements étant négligeables, les tensions ont la même valeur T1=T2=T. En appliquant la deuxième loi de Newton à chaque masse, exprimer les mesures algébriques a1 et a2 des accélérations respectives des masses m1 et m2. Suivant l'axe Oy : T-m1g=m1a1 ; a1 = T/m1 -g. m2g-T=m2a2 ; a2 = g-T/m2. Le fil étant inextensible donner une relation entre a1 et a2. a1 =a2 =a. En déduire l'expression des tensions ainsi que les mesures algébriques des accélérations. T/m1 -g =g-T/m2 conduit à T/m1 +T/m2 = 2g T = 2gm1m2 /(m1+m2). a = T/m1 -g ; a = 2gm2 /(m1+m2) -g ; a =g(m2-m1)/(m1+m2). Que se passe t-il si m2 > m1 ? 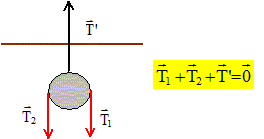L'accélération est positive ; la poulie tourne dans le sens anti-horaire. La tension T' exercée sur la poulie par le fil de suspension au plafond dépend-elle du sens de déplacement relatif des masses ? Non, la masse de la poulie étant négligeable. T' = 2 T   Chariot sur un plan incliné. Fils inextensibles ; poulie sans masse ; frottements négligés. a1 = 30 ° ; a 2 = 60 ° ; m1 = 20 kg ; sin 30 = cos 60 = 0,5 ; sin 60 = cos 30 = 0,866 = 1/1,15 Quel doit être la masse de m2 pour que l'ensemble soit en équilibre ?   La poulie étant sans masse, les tensions sont identiques. T= m2g sin a2 ; T= m1g sin a1 ; m2 sin a2 = m1 sin a1 m2 = m1 sin a1 /sin a2 =20*0,5*1,15 = 11,5 kg.   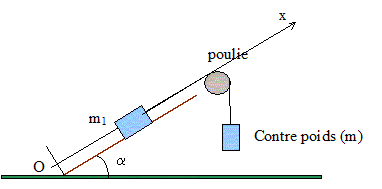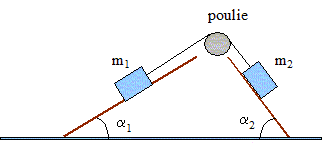Le chariot précédent de masse m1, de centre d'inertie G, est tiré vers le haut sur le même plan incliné à l'aide d'un système à contre poids. La masse de la poulie et les frottements sont négligeables. A l'instant initiale G est en O et sa vitesse est nulle. Faire le bilan des forces subies par le chariot et le contre poids. Quelle condition doit satisfaire m pour que le mouvement soit ascendant ? D'après l'étude précédente, on observe un équilibre si : m = m1 sin a1 /sin a2 avec ici a2=90°. Le mouvement est ascendant si m > m1 sin a1. m > 20*0,5 ; m > 10 kg. Appliquer la seconde loi de Newton et en déduire l'accélération ax de G. -m1g sin a +T= m1ax ; T = m1 ( ax+ g sin a ) mg-T=max ; T = m(g-ax ) m1 ( ax+ g sin a )=m(g-ax ) ; ax= g(m-m1sin a)/ (m1+m). Etablir l'équation horaire régissant le mouvement de G. La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : vx= axt. La position est une primitive de la vitesse et la position initiale est nulle : x = ½axt2. Etablir l'expression de la durée du mouvement de G entre O et un point A d'abscisse xA=d. t =( 2d/ax)½. On étudie le mouvement de g : on mesure à chaque instant la projection sur l'axe Ox ( nommée vx) du vecteur vitesse de G pendant la montée de G le long du plan incliné. 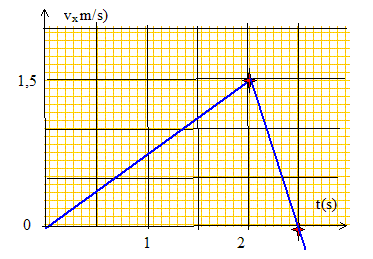A la date t1 = 2,0 s, le fil casse. On trace le graphique vx=f(t). 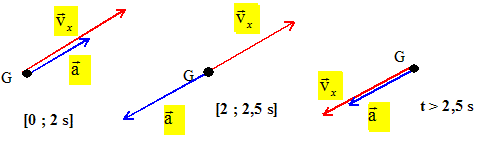Déduire du graphique, sans cacul, la nature du mouvement de G et le sens du déplacement entre les dates 0 - 2s ; 2s - 2,5 s ; t>2,5 s. [0 ; 2 ] : montée ; vitesse positive croissante : mouvement uniformément accéléré. [2 ; 2,5 ] : montée ; vitesse positive décroissante : mouvement uniformément retardé. t =2,5 s ; vitesse nulle : arrêt. t>2,5 s ; vitesse négative : descente du plan, mouvement uniformément accéléré. On précisera sur un schéma les sens des vecteurs vitesse et accélération dans les différentes phases du mouvement. Calculer les valeurs prises par la mesure algébrique de l'accélération de G pour t< 2 s et t> 2s. L'accélération est la dérivée de la vitesse par rapport au temps : cela correspond au coefficient directeur des deux segments de droite du graphe ci-dessus. de 0 à 2 s : a = 1,5/2 = 0,75 m s-2. t > 2 s : a = -1,5 /0,5 = -3,0 m s-2. Quelle distance le chariot a t-il parcourue entre l'instant t=0 et t= 2 s ? x = ½at2 ; x = 0,5*0,75*22 =1,5 m.

retour -menu