Condensateur, iode 131, chute d'un grêlon Concours manipulateur électroradiologie médicale APHP 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

Charge et décharge d'un condensateur. (3pts) Plusieurs réponses sont possibles. Toute erreur annule le point de la question. L'énergie d'un condensateur s'écrit :   E =½Cu2 E=½qu2 E =½q2/C E =½q u vrai vrai L'équation différentielle de la charge d'un condensateur de capacité C par un générateur de force électromotrice E à travers une résistance R est :   E =Rdq/dt + q/C E=Ri +q E =RCdu/dt + u E =Rdu/dt + u vrai vrai Rdu/dt n'a pas la dimension d'une tension i =dq/dt ; Rdq/dt =Ri ; u= q/C q n'a pas la dimension d'une tension RC a la dimension d'un temps La tension aux bornes d'un condensateur de capacité C = 22 nF est u =7,85 V. Quelle est la charge du condensateur ? 2,80 nC 173 nC -2,80 nC vrai q=C u =22 *7,85 = 173 nC  La constante de temps d'un dipôle RC ( R=120 kW ; C=0,22 mF) est :   26,4 s 26,4 ms 1,83 ms vrai t=RC =1,2 105 *2,2 10-7= 2,64 10-2 s = 26,4 ms   La charge d'un condensateur diminue de 12mC en 2,5 ms. L'intensité du courant qui traverse le circuit est : 4,8 mA -4,8 mA 30 nA vrai i =Dq/Dt = -1,2 10-5 *2,5 10-3= -4,8 10-3 s = -4,8 mA L'énergie d'un condensateur de capacité C =560 mF aux bornes duquel existe une tension de 16,0 V est : 8,96 10-3 J 71,7 10-3 J 2,51 10-6 J vrai E =½Cu2 = 0,5*5,6 10-4 *162= 7,17 10-2 J   La glande thyroïde produit des hormones essentielles à différentes fonctions de l'organisme à partir de l'iode alimentaire. Pour vérifier la forme ou le fonctionnement de cette glande, on procède à une scintigraphie en utilisant les isotopes 13153 I ou 12353I de l'iode. Un patient ingère une masse m = 1,00 mg d'iode 131. On donne : Antimoine 51Sb ; Tellure 52Te ; Xénon 54Xe ; césium 55Cs. demi-vie de l'iode 131 : 8 jours ; demi-vie de l'iode 123 : 13,2 heures. A0 = 4,61 109 Bq. Définir le terme isotope. Deux isotopes ont le même numéro atomique ; ils ne se différentient que par leur nombre de neutrons. Calculer ( en Bq) l'activité A de l'échantillon d'isotope 13153 I à l'instant de l'examen pratiqué 4 heures après l'ingestion de l'iode radioactif. On prendra A0 comme activité de l'iode 131 au moment de l'ingestion. Loi de décroissance radioactive A = A0 exp (-lt) avec lt½ = ln2 l = 0,693 / (8*24) =3,61 10-3 heure -1. A = 4,61 109 exp(-3,61 10-3*4) =4,54 109 Bq. On considère maintenant que le patient ingère une quantité d'isotope 12353I telle que l'activité initiale de cet isotope soit A0. L'activité A ( valeur trouvée à la question précédente ) sera t-elle atteinte après une durée identique, plus petite ou plus grande qu'avec l'isotope 13153 I ? Justifier. l = 0,693 / 13,2 =5,25 10-2 heure -1. 4,54 109 =4,61 109 exp(-5,25 10-2 t) ; 0,985 = exp(-5,25 10-2 t) ln 0,985 = -1,53 10-2 = -5,25 10-2 t ; t = 1,53/5,25 =0,29 heure, donc durée plus petite. Evolution temporelle de système mécanique. La grêle se forme dns les cumulo-nimbus où la température est très basse, jusqu'à -40 °C. le grêlon tombe lorsqu'il n'est plus maintenu au sein du nuage. Au sol la vitesse peut atteindre 160 kmh. On étudie un grêlon de masse m qui tombe d'un point O d'altitude 1500 m sans vitesse initiale. Il peut être assimilé à une sphère de r=1,5 cm. Le point O era pris comme origine d'un axe Oz orienté positivement vers le bas. On admettra que le grêlon tombe en chute libre. Volume d'une sphère : V = 4/3 pr3 ; g = 9,80 m/s2 ; masse volumique de l'air ra = 1,3 kg m-3. masse volumique de la glace : rg = 9,2 102 kg m-3. Après avoir énoncé la deuxième loi de newton, déterminer les équation donnant la vitesse et la position du centre d'inertie G du grêlon en fonction du temps. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse m du solide par l'accélération de son centre d'inertie. Dans l'hypothèse d'une chute libre, le grêlon n'est soumis qu'à son poids ; son accélération est l'accélération de pesanteur. La vitesse est une primitive de l'accélération et la vitesse initiale est nulle. v = gt. La position est une primitive de la vitesse et la position initiale est nulle. z = ½gt2. Calculer la valeur de la vitesse lorsqu'il atteint le sol. Conclure. t = v/g d'où z = v2/ (2g) ; v = [2gz]½ =[2*9,8*1500]½ =172 m/s = 172*3,6 km/h = 620 km/h. Ce résultat ne correspond pas à la vitesse observée : l'hypothèse d'une chute libre est fausse. En réalité le grêlon est soumis à d'autres forces, la poussée d'Archimède et la force de frottement fluide de valeur proportionnelle au carré de la vitesse f = k v2. Par une analyse dimensionnelle, déterminer l'unité de k dans le système S.I. k = force / vitesse au carré. force = masse * accélération = masse * longueur / temps2 ; [force]= M L T-2. [vitesse2]= L2T-2 ; [k]=M L-1. Donner l'expression de la valeur de la poussée d'Archimède et du poids en fonction du volume V du grêlon et des masses volumiques. Les calculer et les comparer : conclure. volume V = 4/3*3,14*(1,5 10-2)3 =1,41 10-5 m3. Poids, verticale, vers le bas P=Mg= rgVg. P= 920*1,41 10-5 *9,80 =0,127 N. Poussée d'Archimède, verticale, vers le haut, valeur : poids du volume d'air déplacé : Poussée F= raVg. F= 1,3*1,41 10-5 *9,80 =1,8 10-4 N. P/F = 1270/1,8 ~ 700 ; la poussée est négligeable devant le poids. 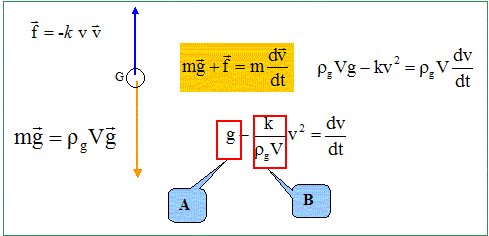Etablir l'équation différentielle du mouvement. Montrer qu'elle peut s'écrire sous la forme dv/dt = A -Bv2. Exprimer littéralement la vitesse limite atteinte par le grêlon en fonction de A et B puis la calculer et conclure. On donne B = 5,2 10-3 S.I. Quand la vitesse limite est atteinte, le mouvement est rectiligne uniforme : dvlim/dt=0. L'équation différentielle s'écrit : A-Bv2lim=0 ; vlim = [A/B]½ = [9,8/5,2 10-3]½=43,6 m/s=43,6*3,6 km/h =157 km/h. En accord avec la valeur observée.

ayon 1,5 cm.

retour -menu