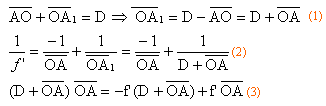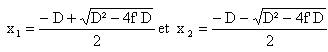|
lentille mince ; méthode de Bessel ; lunette astronomique concours Caplp interne 2008 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
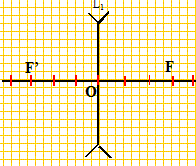
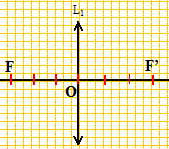
Milieu homogène, isotrope, transparent : au moins l'un des dioptres n'est pas plan. Mince : l'épaisseur de la lentille doit être faible par rapport aux rayons de courbure de chaque dioptre. L' épaisseur de la lentille est inférieure à la valeur absolue de la différence des rayons de courbure de chaque dioptre. Comment peut-on au toucher, distinguer une lentille mince convergente d'une lentille mince divergente ? Une lentille convergente est plus épaisse au centre que sur les bords ; une lentille divergente est plus mince au centre que sur les bords. Représenter la modélisation d'une lentille convergente. Placer le centre optique, le foyer principal objet F et le foyer principal image de cette lentille.
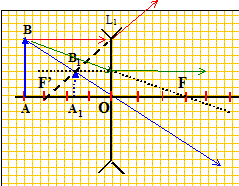
On considère un objet AB réel, perpendiculaire à l'axe optique, A étant sur l'axe optique et OA >OF. Construire l'image A1B1 de l'objet AB par la lentille convergente. Donner le sens et la nature de l'image obtenue.
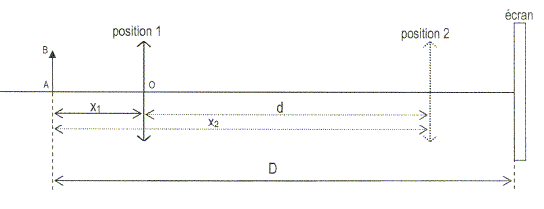
Détermination de la vergence d'une lentille mince. Donner la définition de la vergence d'une lentille mince. Préciser l'unité de cette grandeur. La vergence est l'inverse de la distance focale image, exprimée en mètre. La vergence s'exprime en dioptrie ( d ). Méthode de Bessel : On désire déterminer la distance focale f' d'une lentille convergente. On dispose d'un banc d'optique horizontal, d'un objet réel noté AB, d'une lentille mince convergente L de centre optique O et de distance focale f', d'un écran opaque perpendiculaire à l'axe optique de la lentille et au banc d'optique. L'objet et l'écran étant fixes, distants de D sur le banc d'optique, on cherche à obtenir les deux positions de la lentille pour lesquelles une image nette A'B' se forme sur l'écran. On note d la distance entre les deux positions de la lentille et x la distance entre le centre optique de la lentille et l'objet A ( OA=x).
A partir de la relation de conjugaison d'une lentille mince, montrer que l'on obtient une équation du second degré en x de la forme : x2+Dx+Df'=0.
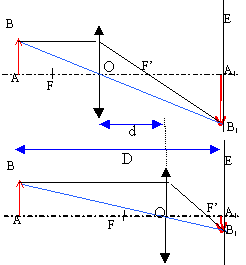
(2) réduction au même dénominateur les dénominateurs étant égaux, il y a égalité entre les numérateurs. on pose mesure algébrique de OA = x. d'où en effectuant : D x +x² = -f' D -f' x + f' x x² + Dx + f'D=0 On impose D>4f'. Exprimer les distances x1 et x2 correspondant aux positions de la lentille pour lesquelles une image se forme sur l'écran. Exprimer f' en fonction de D et d. résoudre l'équation du second degré : D= D²-4f'D le discriminant est positif si D >4f'
la différence x1-x2 est égale à d. élever au carré d'où : d² = D²-4f'D soit (D²-d²) / (4D) = f'. L'écran et l'objet sont distants de 1,50 m ; expérimentalement on mesure x1 = 0,14 m et x2 = 1,36 m. Déterminer la vergence, arrondie à l'unité, de la lentille étudiée. D=1,50 m ; d = x2-x1 = 1,36-0,14 = 1,22 m ; D²-d² = 0,7616 v= 1/f' = 4D/(D2-d2) = 6/0,7616 =7,88 arrondi à 8 d.
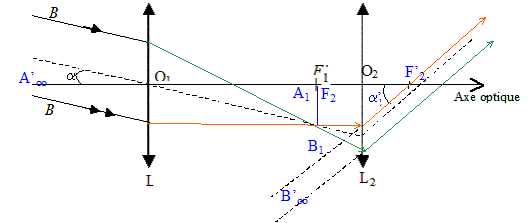
Lunette astronomique. La lunette est constituée d'un objectif et d'un oculaire. On la modélise de la manière suivante :
Expliquer pourquoi on accole les lentilles de vergences respectives +3 d et -2 d pour former l'objectif. La vergence du système constitué par les deux lentilles accolées vaut 1 d : on obtient ainsi une lentille équivalente de distance focale f'=1 m. Caractérisée l'image, obtenue par cet objectif, d'un objet situé à l'infini ( nature, position, sens, grandeur ). L'image d'un objet réel situé à l'infini se trouve dans le plan focal image de l'objectif : l'image est réelle, renversée par rapport à l'objet, plus petite que l'objet. Indiquer le rôle de la lentille de vergence 8 d. oculaire : cette lentille fonctionne comme une loupe. L'image intermédiaire donnée par l'objectif sert d'objet réel pour l'oculaire. La lunette est un système afocal qui donne une image grossie d'un objet à l'infini. Indiquer où se trouve cette image donnée par la lunette. L'image intermédiaire se trouve dans le plan focal objet de l'oculaire ; l'image définitive est à l'infini.
Déterminer la distance entre l'objectif et l'oculaire. distance focale image objectif + distance focale image oculaire = 1 +1/8 =1,12 m.
|
|||||||
|
|
|||||||
|
|
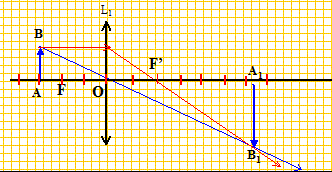 L'image
est réelle, de sens contraire à
l'objet.
L'image
est réelle, de sens contraire à
l'objet.