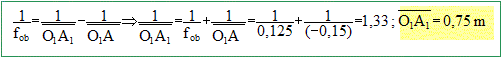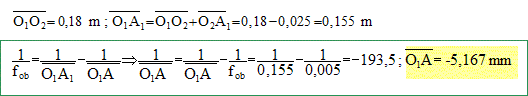Modélisation d'un microscope : latitude de mise au point capes agricole 2004

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

On modélise un microscope par 2 lentilles convergentes. L’objet AB mesure 2,5 mm ; il est placé à gauche de

l’objectif, à 15 cm ; la distance focale de l’objectif est de 12,5 cm et celle de l’oculaire 25,0 cm. On appelle F_ob et F'_ob les foyers de l'objectif et F_oc et F'_oc ceux de l'oculaire.

Les distances algébriques sont écrites en gras et en bleu.

Déterminer par le calcul, la nature, la dimension et la position de l’image A₁B₁ donnée par l’objectif de AB.

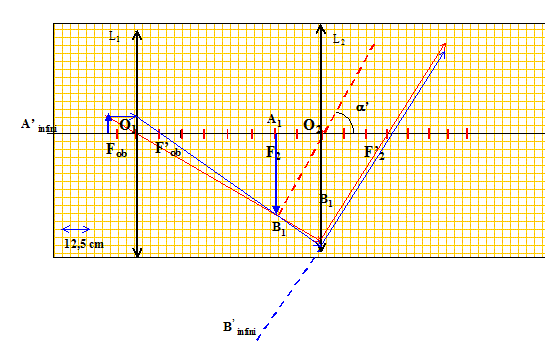
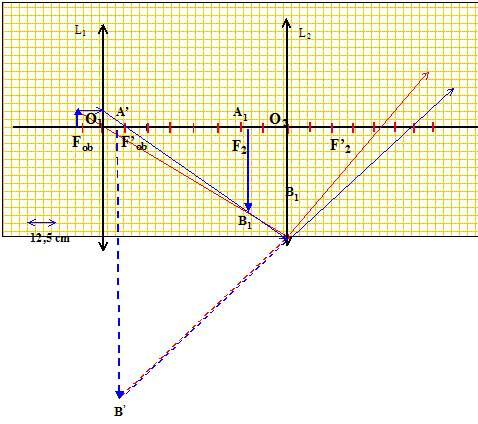
L'image se trouve à droite de la lentille : elle est réelle.

Grandissement latéral : g = O₁A₁ / O₁A = 0,75 / (-0,15) = -5.

Le grandissement étant négatif, l'image est renversée par rapport à l'objet.

A₁B₁ = g AB =-5*2,5 = -12,5 mm.

La distance interfoyers ou intervalle optique D vaut 62,5 cm.

Déterminer par le calcul la nature, la dimension et la position de l’image définitive A'B' de A₁B₁, donnée par l’oculaire.

L'image intermédiaire joue le rôle d'objet pour l'oculaire.

A₁B₁ se trouve au foyer objet de l'oculaire : l'image définitive A'B' est à l'infini.

Cette image est virtuelle, a le sens de A₁B₁.

Retrouver les résultats par une méthode graphique.

On rapproche l’objet AB de 1, 2, puis 3 mm. La distance O₁A ne vaut plus alors respectivement que 14,9 cm, 14,8 cm et 14,7 cm.

Pour chacun de ces trois cas, calculer la distance O₂A₁.

En déduire la distance O₂A’ séparant l’image définitive A’B’ de l’oculaire, dans ces trois cas.

distance O1A	distance O2A1	distance O2A'
14,9 cm	22,4 cm	2,15 m
14,8 cm	19,6 cm	0,91 m
14,7 cm	16,5 cm	0,49 m

Conclure quant à l’influence d’un petit déplacement de l’objet par rapport à l’objectif.

L'image A'B' se rapproche de l'oculaire si l'objet se rapproche de l'objectif.

Construire sur le schéma, avec une autre couleur, la marche des rayons, l’image intermédiaire A₁B₁ et l’image définitive A’B’ dans le cas où AB

s’est rapproché de 2 mm.

Dans les trois cas mentionnés ci-dessus, l’oeil (appliqué à l'oculaire) doit-il accommoder ? Si oui quel est le cas où l’accommodation doit être la plus forte ? Justifier votre réponse en utilisant la formule de conjugaison des lentilles.

 L'oeil doit d'autant plus accomoder que l'objet se rapproche de l'objectif.

Par définition, la latitude de mise au point d’un microscope est l’intervalle des positions donnant une image nette d’un objet fixe. Le calcul de cette grandeur nécessite de connaître la position des objets et des images à 0,1 µm près.

Considérons un microscope dont l’intervalle optique D vaut 15,0 cm, la distance focale de l’objectif 5 mm et celle de l’oculaire 25 mm. Soit un oeil normal (punctum remotum à l’infini) placé au foyer image de l’oculaire. En accommodant au maximum cet oeil peut voir des objets situés à 15 cm de lui.

Calculer, par rapport à l’objectif, la position de l’objet correspondant à une image A’B’ rejetée à l’infini.

A'B' étant à l'infini, A₁B₁ se trouve au foyer objet de l'oculaire.

Déterminer la position de l’image A’B’ vue par l’oeil normal lorsqu’il accommode au maximum.

L'image A'B' se trouve à 15 cm à gauche de l'oculaire.

Calculer la position de A₁B₁ correspondante. En déduire la position de AB par rapport à l’objectif dans ce cas.

Que vaut dans ces conditions la latitude de mise au point de ce microscope ?  

 (5,167-5,145) 10^-3= 2,1 10^-5 m.