Diagramme E pH du chlore ; électrolyse d'une solution de chlorure de sodium capes agricole 2004

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

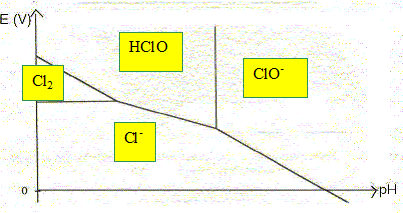
Cl₂ (aq), Cl^-(aq), HClO (aq), ClO_- (aq).

La convention adoptée pour ce tracé est la suivante : sur la frontière entre deux espèces, les concentrations des deux espèces en solution sont, chacune, égales à 0,10 mol.L^-1.

Compléter le diagramme donné en indiquant les domaines de prédominance des espèces considérées.

Déterminer l’abscisse de la frontière entre les deux espèces HClO(aq) et ClO^-(aq).

Donnée : couple acide base HClO / ClO^- : pK_a = 7,5

HClO + H₂O = ClO^- + H₃O⁺ .... K_a =[H₃O⁺ ][ClO^-] / [HClO]

Sur la frontière : [ClO^-] = [HClO] d'où K_a =[H₃O⁺ ] soit pH=pK_a = 7,5.

Déterminer l’expression du potentiel d’oxydoréduction à la frontière correspondant au couple : Cl2(aq) /Cl-(aq). E° (Cl2(aq) /Cl-(aq)) = 1,39 V Cl2(aq) + 2e- = 2 Cl-(aq)) E1 =E° (Cl2(aq) /Cl-(aq)) + 0,03 log ([Cl2(aq)] /[Cl-(aq)]2) ; Sur la frontière : [Cl2(aq)]=[Cl-(aq)] d'où : E1 =E° (Cl2(aq) /Cl-(aq)) + 0,03 log (1 /[Cl-(aq)])= 1,39 +0,03 log10 =1,42 V.

Déterminer le coefficient directeur de l’équation de la frontière entre Cl₂ (aq) et HClO(aq).

E° ( HClO(aq) /Cl₂(aq)) = 1,60 V

2HClO(aq) + 2e^- + 2H⁺ = Cl₂(aq) + 2H₂O

E₂ =E° ( HClO(aq) /Cl₂(aq)) + 0,03 log ([HClO(aq) ]²[H⁺]² /[Cl₂(aq)])

Sur la frontière : [Cl₂(aq)]=[HClO(aq) ] d'où : E₂ =E° ( HClO(aq) /Cl₂(aq)) + 0,03 log ([HClO(aq) ][H⁺]² )

E₂ =E° ( HClO(aq) /Cl₂(aq)) + 0,03 log 0,1 + 0,06 log [H⁺]

E₂ =1,57- 0,06 pH ; pente -0,06 pH.

Élaborer et reporter sur le diagramme potentiel – pH de l’eau en prenant les pressions partielles du dioxygène et du dihydrogène égales à P₀ = 1,00 bar. 

E° ( O2(g) / H2O) = 1,23 V ; O2 +4e- + 4H+ = 2H2O E3 = E° ( O2(g) / H2O) +0,015 log ([H+]4 P2O2) E3 = 1,23 +0,06 log [H+] = 1,23 -0,06 pH. E° ( H+(aq)/ H2(g) ) = 0 V ; 2e- + 2H+ = H2(g) E4 = E° ( H+(aq)/ H2(g) ) +0,03 log ([H+]2 / PH2) E4 =0,06 log [H+] = -0,06 pH.

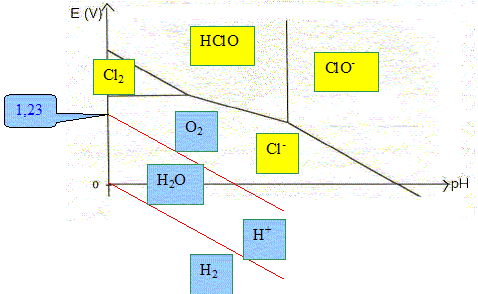
L’élément chlore est utilisé pour désinfecter l’eau des piscines. Une des méthodes actuelles pour réaliser cette opération est de procéder à l’électrolyse d’une solution aqueuse de chlorure de sodium. Les électrodes sont en titane ; les compartiments anodique et cathodique ne sont pas séparés.

Écrire les équations des réactions électrochimiques qui peuvent se produire à chacune des électrodes lors de l’électrolyse, en précisant le nom des électrodes.

A l'anode positive, oxydation de l'eau et /ou de l'ion chlorure :

2H₂O = O₂ +4e^- + 4H⁺ ; 2 Cl^-(aq)) =Cl₂(aq) + 2e^-.

A la cathode négative réduction de l'eau :

2H₂O +2e^- = H₂ + 2OH^- ;

En réalité, on observe un dégagement de dichlore gazeux sur l’une des électrodes et de dihydrogène sur l’autre. Proposer une explication.

L'oxydation de l'eau en dioxygène doit être plus lente que celle de l'ion en chlorure en dichlore. Il faut également prendre en compte les phénomènes de surtension.

Une réaction va se produire en solution aqueuse entre certains des produits de l’électrolyse.

Nommer cette réaction et écrire son équation sachant que le pH des eaux de piscine doit être compris entre 7,0 et 7,4.

dismutation du dichlore en en ion ClO^- et en ion chlorure.

Cl₂(aq) + 2OH^- = ClO^-(aq) + Cl^-(aq) +H₂O.

Quelle est l’espèce chlorée responsable de la désinfection de l’eau de la piscine ?

ClO^-(aq).

Une piscine a pour volume 63 m³. La concentration massique initiale en chlorure de sodium Na Cl est c₀ = 3,1 g.L^-1.

L’intensité moyenne du courant qui traverse l’électrolyseur est égale à I = 11 A.

Calculer, après une année de fonctionnement à raison de 8 heures par jour, la quantité d’ions chlorure consommée par électrolyse.

Quantité d'électricité (C) = intensité (A) * durée (seconde)

Q= I t = 11*3600*8*365 =1,156 10⁸ C.

Quantité de matière d'électrons correspondante : n( e^-) = Q/ 96500 = 1,156 10⁸ /96500 =1,20 10³ mol.

2 Cl^-(aq)) =Cl₂(aq) + 2e^-.

n(Cl^-) = n( e^-) =1,20 10³ mol

masse d'ion chlorure consommés par électrolyse : 1,2 10³*35,5 =4,26 10⁴ g = 42,6 kg.

Si on ne tenait compte que de la consommation des ions chlorure par l’électrolyse, quelle serait la nouvelle concentration massique en chlorure de sodium de l’eau au bout d’un an ?

Masse initiale d'ion chlorure : 3,1*35,5/58,5 = 1,88 g/L ; et dans 63 m³ : 63*3,1*35,5/58,5 = 118,5 kg.

Masse restante : 118,5-42,6 = 75,9 kg.

soit 75,9 / 63 = 1,2 g/L.

Sur le boîtier de la cellule d’électrolyse, on peut lire la recommandation suivante : « Ne pas ouvrir en fonctionnement. Risque d’explosion. ».

Justifier cette recommandation.

L'électrolyse donne du dihydrogène, insoluble dans l'eau. Ce dernier, en présence du dioxygène de l'air constitue un mélange explosif.