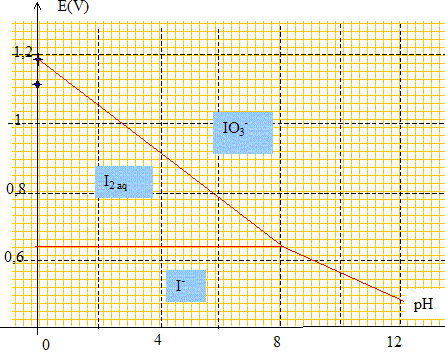
Influence du pH sur la stabilité du diiode en solution aqueuse concours Capes interne 2008 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Déterminer le nombre d'oxydation de l'iode dans l'ion iodate IO3-. n.o(I) +3 n.o(O) = -1 avec n.o(O) - -2 d'où n.o(I) = +V. Soient les deux couples redox IO3- aq/I2aq et I2aq/I-aq. Ecrire les demi-équations électroniques pour ces deux couples. 2IO3- aq+ 12H+aq + 10e- = I2aq+ 6H2O. I2aq+2e- =2I-aq. Expliciter les potentiels d'électrode correspondants : E1 = E°(IO3- aq/I2aq ) + 0,06/10 log([IO3- ]2[H+]12/ [ I2]) E2 = E°( I2aq/I-aq ) + 0,03 log([ I2]/ [I-]2) Le potentiel de Nernst dépend de la température. Justifier. Le potentiel de Nernst découle des potentiels chimiques : ces derniers dépendent de la température. Pour chacun de ces couples, calculer le potentiel de Nernst à pH=0 et à pH=10 à la frontière de prédominance des deux espèces. On prendra les concentrations des espèces considérées égales à 0,100 mol/L sur cette frontière. E°(IO3- aq/I2aq ) = 1,19 V ; E°( I2aq/I-aq ) = 0,62 V. E1 = 1,19 + 6 10-3 log([0,1]2[H+]12/ [ 0,1]) = 1,19 + 6 10-3 log 0,1 + 6 10-3 *12 log [H+] E1 = 1,19 - 6 10-3 +0,072 log [H+] ; E1 = 1,18 - 0,072 pH. à pH 0 : E1 = 1,18 V ; à pH=10 : E1 = 0,464 V ;  E2 = 0,62 + 0,03 log([ 0,1]/ [0,1]2) = 0,62 +0,03 log 10 ; E2 =0,65 V. Tracer les diagrammes de prédominance des espèces relatives à ces couples et conclure quand à la stabilité du diiode à ces pH. IO3- aq+ 6H+aq + 6e- = I- aq+ 3H2O. E3 =E°(IO3- aq/ I- aq) + 0,01 log([IO3- ][H+]6/ [ I- ]) E3 =E°(IO3- aq/ I- aq) + 0,01 log ([IO3- ]/ [ I- ]) -0,06 pH A pH =0 le diiode est stable en solution ; à pH=10 le diiode s'est dismuté en ion iodure et en ion iodate. On dispose d'un volume V=100,0 mL d'une solution de pH=10 contenant n1 = 1,00 10-4 mole d'iodate de sodium (Na+ ; IO3-) et n2 = 2,00 10-2 mol d'iodure de potassium (K+ ; I-). Ces deux solides sont totalement solubles dans l'eau. Que se passe t-il si on acidifie, sans variation de volume, la solution jusqu'à pH=0 ? Médiamutation : obtention d'un degré d'oxydation intermédiaire à partir de composés de degrés d'oxydation différents. 2IO3- aq+ 12H+aq + 10e- = I2aq+ 6H2O.(2) 10I-aq= 5I2aq+10e-. (3) (2) + (3) donne : IO3- + 5I- + 6 H+= 3I2 + 3H2O. (4) Calculer la constante d'équilibre correspondante. K = [I2]3 /([IO3-][I-]5[H+]6). E1 = E°(IO3- aq/I2aq ) + 0,06/10 log([IO3- ]2[H+]12/ [ I2]) E2 = E°( I2aq/I-aq ) + 0,03 log([ I2]/ [I-]2) A l'équilibre E1 =E2 : E°(IO3- aq/I2aq ) + 0,06/10 log([IO3- ]2[H+]12/ [ I2]) = E°( I2aq/I-aq ) + 0,03 log([ I2]/ [I-]2) E°(IO3- aq/I2aq ) - E°( I2aq/I-aq ) = 0,03 log([ I2]/ [I-]2) -0,006 log([IO3- ]2[H+]12/ [ I2]) E°(IO3- aq/I2aq ) - E°( I2aq/I-aq ) =0,006 log ([ I2]6/ ([IO3- ]2[H+]12[I-]10)) E°(IO3- aq/I2aq ) - E°( I2aq/I-aq ) =0,012 log K log K = (1,19-0,62) / 0,012 ; log K= 47,5 ; K = 3,2 1047. Valeur très grande, la réaction est quantitative. Quelle concentration maximale en diiode peut-on obtenir ? "n1 = 1,00 10-4 mole d'iodate de sodium (Na+ ; IO3-) et n2 = 2,00 10-2 mol d'iodure" L'ion iodate est en défaut ( réactif limitant) . D'après les nombres stoechiométriques de (4) : n(I2 )= 3 n(IO3-) = 3n1 = 3,00 10-4 mole de diiode dans V= 0,100 L [I2]max = 3,00 10-3 mol/L. Quel doit être le pH de la solution pour obtenir 90% de cette concentration maximale en diiode ? [I2] =0,9 [I2]max = 2,70 10-3 mol/L soit xf = [I2] *V =2,70 10-4 mol avancement (mol) IO3- + 5I- + 6 H+ = 3I2 + 3H2O initial 0 n1 n2 0 solvant en large excès en cours x n1-x/3 n2-5/3x x fin xf =2,70 10-4 n1-xf /3 =10-5 n2-5/3xf = 1,955 10-2 xf [I-] = 1,955 10-2 / 0,1 = 0,1955 mol/L ; [IO3-] =10-5/0,1 =10-4 mol/L L'expression de K donne : [H+]6 = [I2]3/(K [IO3-][I-]5. [H+]6=( 2,70 10-3)3/[1047,5*10-4*0,19555]= 0,697 10-48. [H+] = 0,94 10-8 ; pH= 8,0.

retour -menu