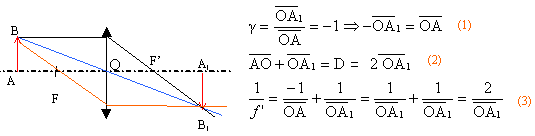|
Spectre, laser, miroir plan, mesure d'une focale ; diffraction ; limite de résolution du microscope : critère de Rayleigh Concours Capes externe 2008 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||||||
| .
. |
|||||||||||
|
|||||||||||
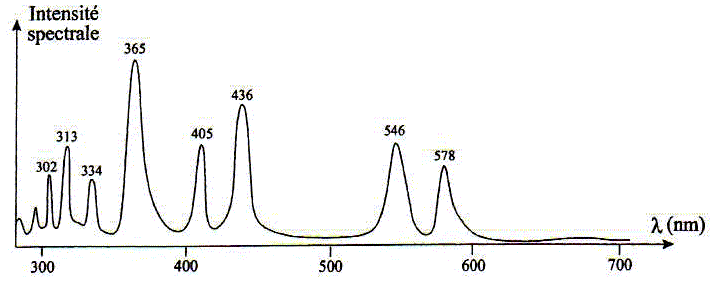
la figure ci-dessous donne le profil d'intensité spctrale simplifié d'une lampe à vapeur de mercure :
Définir le terme "spectre lumineux". Un système dispersif ( prisme) décompose une lumière complexe en un ensemble continu ou discontinu de couleurs : on obtient un spectre. Le spectre ci-dessus donne l'amplitude de chaque couleur d'une lumière complexe en fonction de la fréquence. Comment visualiser sur un écran le spectre de la lampe à vapeur de mercure ? Entourer la lampe d'un cylindre de carton noir percé d'une fente ( 2mm de large, 4 cm de hauteur. Obtenir un faisceau de lumière parallèle en utilisant des lentilles. Interposer sur le faisceau, un réseau 600 traits. Projeter sur un écran.
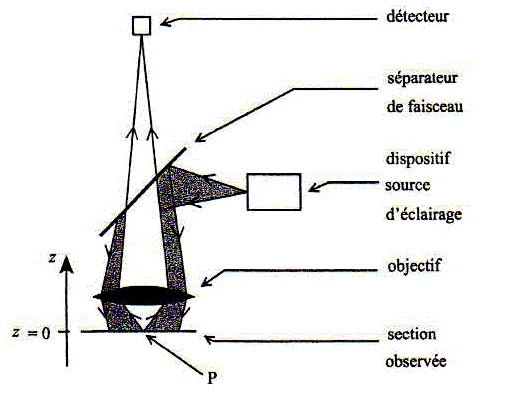
L'objectif du microscope : optique géométrique. L'objectif a un double rôle : il assure le bon éclairage de l'échantillon étudié et, d'autre part, il conjugue un point P de celui-ci au détecteur. On s'intéresse ici à la mesure expérimentale de la distance focale de l'objectif, modélisé par une lentille mince convergente. Définir ce qu'est la distance focale d'une lentille mince. Distance entre le cente optique O et le foyer principal image F' ; la distance focale en mètre est l'inverse de la vergence en dioptrie. Enoncer les conditions de Gaus et la formule de conjugaison de Descartes. Pour obtenir de bonnes images, l'objet doit être de petites dimensions et placé au voisinage de l'axe optique de la lentille. On élimine les rayons trop inclinés sur l'axe optique en diaphragmant. Les distances algébriques sont écrites en gras et en bleu. 1/OF' = 1/OA' - 1/OA. Citer les noms de deux méthodes classiques permettant la mesure de la distance focale d'une lentille mince convergente. Décrire l'une de ces méthodes. Besel, Silbermann. méthode de Silbermann .
L'image donnée par une lentille convergente
à la même taille que
l'objet. relation (2) : la distance objet image est notée D relation (3) : formule de conjugaison des lentilles pour conclure il suffit de remplacer OA1 par ½D, puis de prendre l'inverse des rapports égaux d'où f ' = D/4.
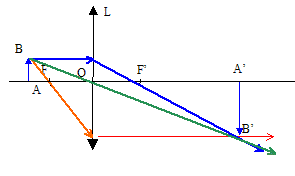
Un ojectif de microscope a t-il une distance focale plutôt grande ou plutôt faible. Faible. Pourquoi les méthodes précédentes sont-elles peu adaptées pour la mesure de la distance focale de l'objectif du microscope ? L'ojectif du microscope ayant une grande ouverture numérique, ne peut pas être assimilé à une lentille mince. On propose une méthode de mesure de la distance focale f' de l'objectif. On modélise l'objectif par une lentille mince de distance focale f' ; l'objet est une mire placé perpendiculairement à l'axe optique de l'objectif ( en amont de son foyer objet). Elle est constituée de graduations de pas a= 0,1 mm et de sous graduations. Elle est éclairée en lumière blanche. On visualise sur un écran l'image de cette mire par l'objectif qui a un pas a' que l'on mesure. Faire un figure représentant la lentille, un point objet B quelconque de la mire, son image b' et les rayons de construction de celle-ci.
Quel est le signe du grandissement g ? Image et objet sont de sens contraire : le signe du grandissement est le signe moins. Trouver l'expression de g en fonction de f' et de la distance p' entre la lentille et l'écran. En déduire que f' = p'/ (1-g). O pose OA = p, OA'=p' : la formle de conjugaison s'écrit : 1/f' = 1/p' -1/p ; 1/f'= (p-p') / (pp'). Le grandisement transversal s'écrit : g =A'B'/AB=p'/p ; p = p'/g . 1/ f'= (p'/g-p') / (p'p'/g)= (1/g-1) / (p'/g)=(1-g)/p' ; f' = p'/ (1-g). Quelle est l'expression de l'incertitude relative Df'/f' sur la distance focale ? log f' = log p' - log (1-g) ; dérivée logarithmique : df'/f' = dp'/p' +dg/(1-g) Df'/f' = D p'/p' +Dg/(1-g) ; Df'/f' =[(D p'/p')2+(Dg/(1-g))2 ]½. A.N : p' = 280 + ou - 15 mm ; a' = 1,75 + ou - 0,05 mm ; a = 0,1 mm. g = -a'/a =-1,75 / 0,1 = -17,5 ; f' = 280/18,5 = 15,13 mm. D p'/p' =15/280 =0,053 ; Dg/g = Da'/a' ; Dg = g Da'/a' =-17,5*0,05/1,75 =-0,5 ; Dg/(1-g) = 0,5/18,5 =0,027. Df'/f' =0,06 ; Df' = 15,13*0,06 =.0,9 ; f' = 15,1 + ou - 1 mm. 15,0 mm < f' <15,2 mm. L'objectif des lunettes de vue a une distance focale de quelques dizaines de centimètres à 1 m. On peut lire sur l'objectif qu'il possède un grandissement x10. Cela veut dire que le grandissement absolu obtenu pour une image formée par l'objectif à la distance D = 16 cm au delà de son foyer image équivalent est gobj =10. Quelle est la distance focale associée avec la lecture du grandissement x10 ? p' = f'+160 mm ; f' = f'+160 / 11 ; 10 f' = 160 ; f' = 16 cm, valeur différente de celle déterminée expérimentalement.
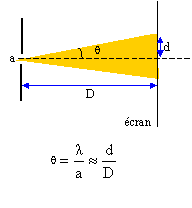
Résolution optique du microscope : L'ouverture numérique de l'objectif du microscope est par définition w0=n sin u où n est l'indice du milieu dans lequel plonge l'objectif et u l'angle maximum par rapport à l'axe optique des rayons isus de P arrivant sur l'objectif. Calculer en degrés l'angle maximum um dans le cas de l'ojectif x10, d'ouverture numérique w0=0,25, plongé dans l'air. nair = 1 ; sin um = w0 = 0,25 ; um =0,252 rad = 0,252*180/3,14 degrés ; um = 14,5 °. Le microscope est plus performant pour la visualisation des détails de l'échantillon avec un objectif x100 d'ouverture numérique w0 =1,30, plongé dans l'huile ( indice n= 1,52). Calculer en degrés l'angle um. sin um =1,30/1,52 =0,855 ; um =1,026 rad = 1,026*180/3,14 ° ; um = 58,8°. Le microscope n'est plus utilisé dans les conditions de Gaus ; par contre sa résolution augmente, sa profondeur de champ décroît. Définir la notion de stigmatisme. Stigmatisme rigoureux : les rayons incidents issus d'un point objet doivent converger en un point unique après traversée de l'instrument d'optique. Stigmatisme approché : les rayons incidents issus d'un point objet doivent converger en une petite tache après traversée de l'instrument d'optique. Quel type d'aberrations doit-on corriger dans ce cas ? Aberrations géométriques. On suppose, pour la suite, que l'objectif est suffisamment corrigé du type précédent d'aberrations ; le microscope est dit limité en résolution par la diffraction. Qu' appelle t-on limite de résolution ou pouvoir séparateur d'un instrument d'optique ? Angle minimal sous lequel deux points très proches peuvent être distingués. Décrire une expérience réalisable en classe permettant de mettre en évidence le phénomène de diffraction. De quels paramètres dépend la diffraction dans cette expérience ? On place perpendiculairement au faisceau lumineux et à quelques centimètres du laser, une fente fine et horizontale de largeur a. Un écran situé à une distance D de la fente, montre des taches lumineuses réparties sur une ligne verticale. La tache centrale plus lumineuse que les autres, est la plus large. 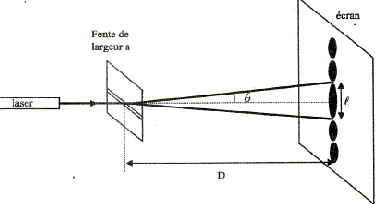
la diffraction dépend de la largeur de la fente et de la longueur d'onde de la lumière. L'angle q est donné par la relation : q =l/a ou demi écart angulaire correspondant à la tache centrale de diffraction. l et a s'expriment en mètre et q en radian.
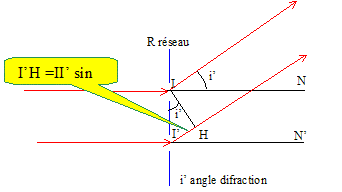
Pour évaluer la limite de résolution du microscope, on met à la place de l'échantillon un réseau périodique de pas d, éclairé en incidence normale par une lumière monochromatique cohérente de longueur d'onde l0. Le réseau est plongé dans un milieu d'indice n. Montrer que le réseau diffracte la lumière dans des directions données par les angles ik ( k entier relatif) par rapport à la normale tels que : sin ik = kl0/(nd).
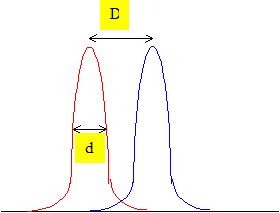
La différence de marche est d=I'H =d sin i'. Les interférences sont constructives dans la mesure où la différence de marche est un multiple de l0/n. d sin ik = kl0/n soit : sin ik = kl0/(nd) avec k entier relatif. Or |sin ik | est inférieur ou égal à 1 : seul un petit nombre de valeurs de k est possible. Qu'observe t-on avec le microscope si on ne laisse passer que l'ordre k=0 du réseau ? Il n' y a pas de diffraction pour k=0 : le réseau ne sert à rien pour k=0 ; pour observer les détails liés à la diffraction il faut prendre k =1 ou 2... En déduire une estimation de la limite de résolution du microscope en fonction de l0 et w0. L'ouverture numérique w0 doit au moins être égale à sinik avec k = 1. sin i1 = sin u ; l0/(nd) = w0/n soit w0=l0/d. La limite de résolution vaut : l0/w0. En pratique, en microscopie confocale, c'est l'objectif qui limite la résolution du microscope et le critère de Rayleigh indique que la limite de résolution est de l'ordre de dmin = 0,5 l0/w0. Expliquer, schéma(s) à l'appui, ce qu'est le critère de Raleigh.
D : distance des pics de diffraction centrés sur les images de détails ; d : largeur des pics à mi-hauteur ; on distingue les détails si D > d. Comment améliorer le pouvoir séparateur du microscope ? Augmenter l0 ; diminuer w0. Calculer la limite de résolution pour l0 =632,8 nm pour l'objectif x10 dans l'air et l'objectif x100 dans l'huile. Dans l'air w0 = 0,25 ; dmin = 0,5 l0/w0 = 0,5*632,8 /0,25 =1265 nm ; dmin = 1,3 mm. Dans l'air w0 = 1,305 ; dmin = 0,5 l0/w0 = 0,5*632,8 /1,30 =243 nm ; dmin = 0,24 mm. |
|||||||||||
|
|
|||||||||||
|
|