Complexation des ions chrome III par l'EDTA. BTS biotechnologie 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

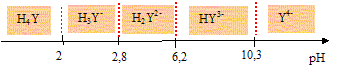
Tous les ions sont hydratés en solution aqueuse. On se propose d'étudier la réaction de complexation des ions Cr3+ (aq) par l'E.D.T.A. en solution aqueuse maintenue à pH = 5,1. L'E.D.T.A. est un tétra-acide noté H4Y dont les pKa en solution aqueuse sont respectivement : H4Y / H3Y- pKa1 = 2,0 ; H3Y- /H2Y2- pKa2 = 2,7 ; H2Y2- / HY3- pKa3 = 6,2 ; HY3- / Y4- pKa4 = 10,3. Tracer le diagramme donnant sur une échelle de pH, les domaines respectifs des diverses espèces majoritaires. Quelle est en conséquence l'espèce prédominante dans cette solution aqueuse sachant que son pH vaut 5,1 ?  A pH =5,1, la forme H2Y2- est majoritaire. L'équation de la réaction de complexation à pH = 5,1 s'écrit sous la forme : Cr3+ + H2Y2- = CrY- + 2 H+. Le complexe CrY- formé est très stable. La transformation est lente et totale ; elle est d'ordre 1 par rapport aux ions Cr3+ et d'ordre 1 par rapport aux ions H2Y2- . La constante de vitesse est notée k. La solution contient initialement : - des ions H2Y2- de concentration molaire [H2Y2-]0 = 0,100 mol.L-1 et - des ions Cr3+ de concentration molaire [Cr3+]0 = 3,00 ×10-3 mol.L-1. On suit le déroulement de la réaction à température, volume et pH constants en mesurant la quantité de complexe formé et on obtient le tableau suivant t(min) 0 10 20 30 40 60 90 120 [CrY-] mol/L 0 0,240 10-3 0,450 10-3 0,655 10-3 0,840 10-3 1,17 10-3 1,57 10-3 1,88 10-3 Donner l'expression de la vitesse de la réaction en fonction de k et des concentrations en ions Cr3+ et H2Y2-. v = k[Cr3+][H2Y2-].   Calculer la concentration en ions H2Y2- en fin de réaction ; comparer cette valeur à la valeur initiale de la concentration en ions , [H2Y2-]0 = 0,100 mol.L-1. Tableau établi pour 1 L de solution. avancement (mol) Cr3+ + H2Y2- = CrY- + 2 H+ initial 0 [Cr3+]0 [H2Y2-]0 0 0 en cours x [Cr3+]0 -x [H2Y2-]0-x x 2x fin xmax [Cr3+]0-xmax [H2Y2-]0-xmax [CrY-]f =xmax 2xmax 3,00 ×10-3 0 9,7 10-2 3,00 ×10-3 6,00 ×10-3 Si Cr3+ est en défaut : [Cr3+]0-xmax =0 ; xmax =[Cr3+]0 = 3,00 ×10-3 mol.L-1. Si H2Y2- est en défaut : [H2Y2-]0-xmax=0 ; xmax=[H2Y2-]0 = 0,100 mol.L-1 On retient la plus petite valeur. [H2Y2-]fin ~ [H2Y2-]0. La concentration en ions H2Y2- peut être considérée comme constante au cours de la réaction. Donner alors une expression simplifiée de la vitesse de la réaction en introduisant une constante k' que l'on définira. Quel est alors l'ordre apparent de la réaction par rapport au réactif Cr3+ ? v = k[Cr3+][H2Y2-] = k'[Cr3+] avec k' = k[H2Y2-]0 =0,1 k. Établir par un simple bilan de matière la relation reliant les concentrations molaires des espèces chimiques Cr3+ et CrY- à l'instant de date t. Le tableau d'avancement ci-dessus conduit à : [Cr3+]t =[Cr3+]0 -x = [Cr3+]0 -[CrY-]t .   Consigner dans un tableau les huit valeurs numériques de [Cr3+] pour chacune des dates t figurant dans le tableau ci-dessus. On suppose que la disparition des ions Cr3+ suit une loi de vitesse du premier ordre. t(min) 0 10 20 30 40 60 90 120 [CrY-] mol/L 0 0,240 10-3 0,450 10-3 0,655 10-3 0,840 10-3 1,17 10-3 1,57 10-3 1,88 10-3 [Cr3+]t =[Cr3+]0 -[CrY-] [Cr3+]0 = 3 10-3 2,76 10-3 2,55 10-3 2,34 10-3 2,16 10-3 1,83 10-3 1,43 10-3 1,12 10-3 [Cr3+]0 /[Cr3+]t 1 1,086 1,176 1,28 1,39 1,64 2,10 2,68 ln([Cr3+]0 /[Cr3+]t ) 0 0,083 0,162 0,248 0,328 0,484 0,74 0,985 k'= ln([Cr3+]0 /[Cr3+]t ) /t xxxx 8,3 10-3 8,1 10-3 8,3 10-3 8,2 10-3 8,2 10-3 8,2 10-3 8,2 10-3 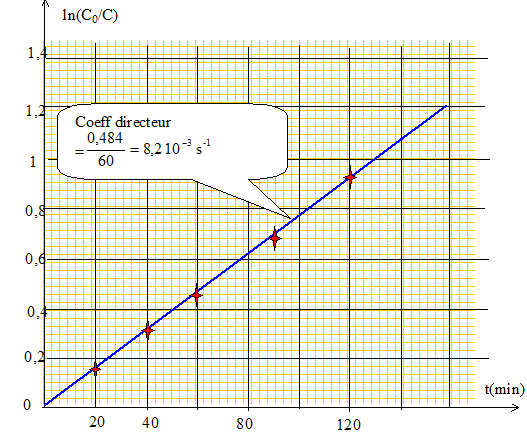Donner sans démonstration la relation entre le temps t écoulé depuis le début de la réaction, la valeur correspondante [Cr3+] de la concentration des ions Cr3+ et la valeur initiale de la concentration en ions Cr3+, [Cr3+]0. ln([Cr3+]0 /[Cr3+]t ) = k' t. Montrer par une méthode graphique que la cinétique est d'ordre 1 par rapport aux ions Cr3+. On prendre obligatoirement pour échelle : 1 cm pour 10 minutes, 10 cm pour une unité logarithmique. En déduire la valeur de la constante k'. Préciser son unité. k' =8,2 10-3 s-1. En déduire la valeur de la constante k. Préciser son unité.  k' = k[H2Y2-]0 =0,1 k. k = 8,2 10-2 L mol-1 s-1.

retour -menu