circuit RLC bac STL chimie de laboratoire et procédés industriels 2008.

. .

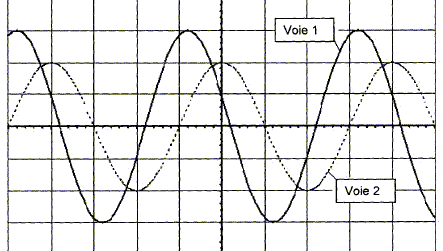
Lors d'une séance de travaux pratiques, on dispose du matériel suivant pour réaliser un circuit RLC série : - un générateur basse fréquence ; - un conducteur ohmique de résistance R= 220 W ; - un condensateur de capacité C inconnue; - une bobine d'inductance L= 0,450 H et de résistance consodérée comme nulle; - un oscilloscope. 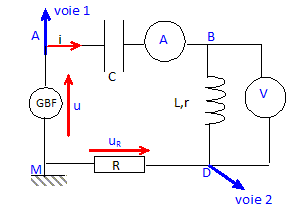Pour une certaine fréquence de la tension délivrée par le générateur, on obtient l'oscillogramme suivant : voie 1 : tension u(t) aux bornes du dipôle RLC, courbe en trait plein voie 2 : tension uR(t) aux bornes du conducteur ohmique R, courbe en pointillés Base de temps : 1,0 ms / div ; voie 1 : 2 V / div ; voie 2 : 1 V / div. Faire un schéma du circuit étudié et indiquer les branchements de l'oscilloscope pour observer les courbes u(t) et uR(t).  Ajouter les appareils qui permettraient de mesurer la tension aux bornes de la bobine et l'intensité du courant dans le circuit. Etude de l'oscillogramme. Déterminer les valeurs de la période, de la fréquence et de la pulsation du signal délivré par le générateur. période T = 4,0 10-3 s. Fréquence f = 1/T = 1/4,0 10-3 =2,5 102 Hz. Pulsation w = 2p f = 6,28*250 =1,57 103 |~1,6 103 rad/s. Déterminer les valeurs efficaces U et UR des tensions visualisées. U = Umax / 2½ =6/ 2½ = 4,2 V. UR = UR max / 2½ =2/2½ = 1,4 V. En déduire la valeur de l'intensité efficace I du courant dans le circuit. I =UR /R = 1,4 / 220 =6,4 10-3 A. Déterminer le déphasage j de la tension u(t) par rapport à l'intensité i(t). Préciser et justifier son signe. j = 0,2 T soit 0,2 * 2p = 0,4p radian. La courbe u(t) est en avance sur uR(t) donc sur l'intensité i(t). 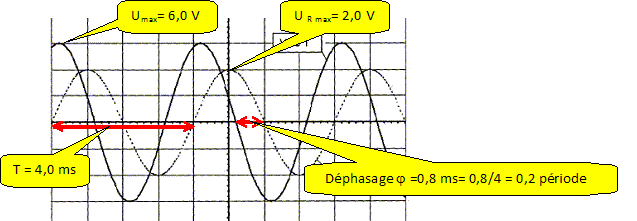Déduire des résultats précédents : - l'expression de la tension u(t) et de l'intensité i(t) en prenant la tension u(t) comme origine des phases. u(t) = 6 sin ( wt) = 6 sin (1,6 103 t). i(t) = UR max / R sin ( wt- j) = 2/220 sin ( 1,6 103t- 0,4p) = 9,1 10-3 sin ( 1,6 103t- 0,4p). - le caractère capacitif ou inductif du circuit. La tension aux bornes d'un condensateur est en retard sur l'intensité ; la tension aux bornes de la bobine inductive est en avance sur l'intensité. L'intensité i(t) étant en retard sur la tension u(t), le dipole est inductif. - la valeur de l'impédance du dipôle RLC. Z = U/I =4,2/6,4 10-3 =6,6 102 W. La valeur de la capacité du condensateur. Z2 = R2 +(Lw-1/(Cw)2 ; Lw-1/(Cw) = (Z2 - R2)½ = (6602 - 2202)½ =622,2 1/(Cw) = 0,45*1570-622,2= 84,3 ; Cw=1/84,3 = 1,186 10-2 ; C = 1,186 10-2/1570 =7,6 10-6 F.   On modifie la fréquence de la tension délivrée par le générateur tout en maintenant constante sa valeur efficace. Pour une fréquence de 86,5 Hz, les deux tensions visualisées sont en phase. Donner le nom du phénomène observé. Résonance d'intensité. Retrouver la valeur de la capacité C du condensateur. A la résonance d'intensité LCw2=1. C = 1/(Lw2) avec w = 2p f =6,28*86,5 =543,2 rad/s. C = 1/(0,45*543,22) =7,5 10-6 F. Indiquer à cette fréquence la valeur de l'impédance du circuit. L'impédance est minimale, égale à la résistance R du circuit : 220 W. En déduire la valeur de l'intensité efficace du courant. U étant constant, Z étant minimale, l'intensité est maximale : I = U/R = 4,2 / 220 =1,9 10-2 A.

retour -menu