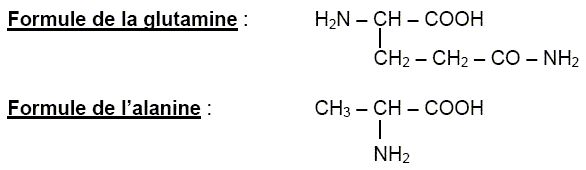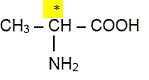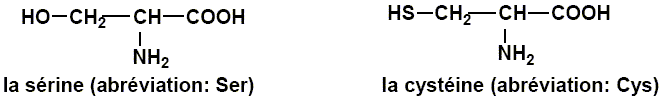synthèse peptidique ; eau oxygénée ; pression dans un liquide et dans un gaz bac SMS France septembre 2005.

. .

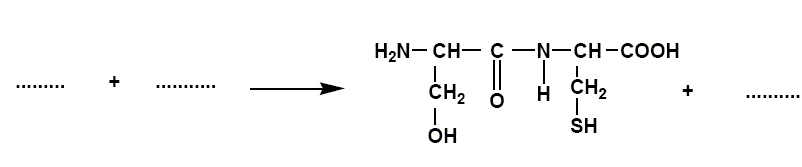
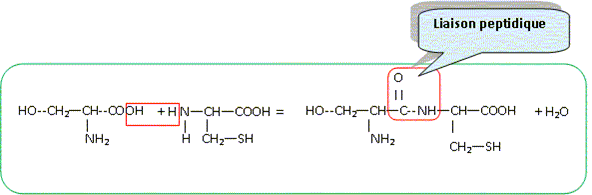
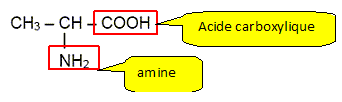
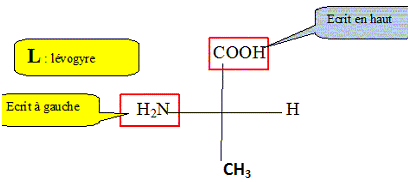
Acide a aminé : dipeptide : Un dipeptide est formé à partir de L-alanine et de L-glutamine. Sur la formule de l'alanine repérer les groupes caractéristiques amine et acide carboxylique. A quelle famille chimique appartient l’alanine ? L'alanine est un acide a-aminé ? Le groupe amine NH2 et le groupe acide carboxylique COOH sont portés par le même atome de carbone. Cette molécule possède un atome de carbone asymétrique. Que signifie cela ? Indiquer cet atome par un astérisque (*) ajouté sur la formule de la molécule.    Un atome de carbone asymétrique : - est un atome de carbone tétragonal ( 4 directions de liaison) - les 4 substituants ( groupes liés à ce carbone) sont différents. Représenter en projection de Fischer la configuration L de l'alanine.   Comment se nomme l’autre isomère de l’alanine ? configuration D de l'alanine. On souhaite synthétiser le dipeptide Ser - Cys en partant d'un mélange des 2 acides a-aminés qui le constituent : Recopier et compléter l'équation-bilan correspondant à la synthèse du dipeptide ci-dessous: Donner le nom du groupe fonctionnel apparu lors de la formation du dipeptide. L’entourer sur la formule. Au cours de cette synthèse, d’autres dipeptides sont apparus simultanément. Combien de dipeptides a-t-on obtenu globalement ? Quatre. Donner le nom de chacun en utilisant les abréviations Ser et Cys. Ser-Cys ;  Cys-Ser ; Ser-Ser et Cys-Cys. L'eau oxygénée. L’eau oxygénée, antiseptique d’usage courant, est une solution de peroxyde d’hydrogène qui se décompose très lentement à température ordinaire. Quelle est la formule du peroxyde d’hydrogène ? H2O2 . Les demi-équations électroniques intervenant dans cette décomposition sont : H2O2 + 2 H+ + 2 e- = 2H2O (1). H2O2 = O2 +2 H+ + 2 e- (2). Ecrire le couple oxydant / réducteur mis en jeu dans l’écriture de la demi-équation 1. H2O2 /H2O. A partir des deux demi-équations précédentes, écrire l’équation-bilan de la réaction de dismutation de l’eau oxygénée.  (1) +(2) donne : H2O2 +H2O2 + 2 H+ + 2 e- = 2H2O +O2 +2 H+ + 2 e- simplifier : 2H2O2 = 2H2O +O2. . Lorsqu’on désinfecte une plaie à l’eau oxygénée, celle-ci subit la réaction de dismutation évoquée provoquant un dégagement gazeux. Citer le nom du gaz produit par la réaction de dismutation de l’eau oxygénée. dioxygène O2. Lors de l’usage externe de l’eau oxygénée sur une peau lésée, on utilise une solution d’eau oxygénée à 10 volumes. Recopier et compléter la phrase suivante : Une eau oxygénée a un(e) titre de 10 volumes si 1 L de cette solution peut libérer, par décomposition totale, 10 L de dioxygène, volume mesuré dans les conditions normales de température et de pression. Le volume d’eau oxygénée à 10 volumes contenu dans un flacon est V = 125 mL. Déterminer le volume V(O2) de dioxygène que peut libérer la décomposition totale de cette eau oxygénée. 125 mL = 1/8 L d'où : 10/8 = 1,25 L. La relation T = 11,2 . c est propre aux solutions aqueuses de peroxyde d’hydrogène. Quelles sont les grandeurs correspondant aux symboles T et c ? Préciser leurs unités respectives. T : titre en L ; c : concentration en mol/L. Calculer alors la valeur de c pour l’eau oxygénée d’usage courant à 10 volumes. c= T/11,2 = 10/11,2 = 0,89 mol/L. Quelle quantité de matière n de peroxyde d’hydrogène est donc dissoute dans le flacon d’eau oxygénée à 10 volumes de volume V = 125 mL ? (n sera exprimé en moles) n= 0,89 *125/1000 = 0,89 /8 =0,11 mol. Pression dans un liquide et dans un gaz. On rappelle que la différence de pression pA - pB entre deux points A et B d'un même fluide au repos (liquide ou gaz) s'exprime par la relation : pA - pB = r . g. h. Indiquer ce que représentent les lettres r et h dans la relation précédente et préciser les unités respectives de pA - pB , r et h dans le systeme international S.I. pA - pB : pression en pascal (Pa) ; r : masse volumique du fluide (kg m-3) ; h : différence de hauteur entre A et B ( m). Quelles doivent être les positions respectives des points distincts A et B pour que pA = pB ? A et B sont dans le même plan horizontal. Des points A et B, lequel est situé le plus bas dans le même fluide au repos pour que l'on ait pA > pB ? A est situé en dessous de B. Un plongeur en apnée se trouve dans la mer de telle manière à ce que son tympan T soit situé à une profondeur h = 10 m par rapport à la surface de la mer. Montrer que la différence de pression pT - pM entre le tympan T et un point M de la surface de la mer supposée au repos est voisine de 101000 Pa. masse volumique de l'eau de mer : 1030 kg m-3; g = 9,8 N/kg. pT - pM = r . g. h =1030*9,8*10 =10 940 ~ 101 000 Pa. Déduire de la question précédente la pression pT qui s’exerce sur le tympan du plongeur si la pression atmosphérique au niveau de la mer vaut pM = 101300 Pa. pT = pM +101 000 = 101 300+101 000 =202 300 Pa. On rappelle que la pression p exercée par une force pressante F sur une surface pressée d'aire S est donée par la relation p = F / S. Indiquer les unités du système international S.I dans lesquelles s'expriment les grandeurs de la relation précédente. p : pression en pascal (pa) ; F : force en newton (N) ; S : aire en m2. En admettant que la pression au niveau du tympan du plongeur est pT = 202000 Pa, calculer la force pressante F qui s'exerce sur le tympan de surface S = 0,5.10-4 m2. F = p .S = 202 000*0,5 10-4 = 10,1 N~ 10 N. Une personne P se trouve dans un bateau à la hauteur h = 10 m au dessus des points M de la surface de la mer dans laquelle évolue le plongeur. Montrer que la différence de pression pM - pP entre M et P est voisine de 127 Pa, sachant que la masse volumique de l'air est voisine de 1,3 kg/m3. pM - pT = r . g. h =1,3*9,8*10 = 127 Pa. Comparer les variations de pression pT - pM et pM - pP de la pour une même hauteur de fluide (eau de mer ou air) et conclure. Faire le rapport des pressions et le rapport des masses volumiques :101000 / 127 ~ 800 ; 1030/1,3 ~ 800. A hauteur égale, la différence de pression entre 2 points d'un fluide homogène au repos, est proportionnelle à la masse volumique du fluide.

retour -menu