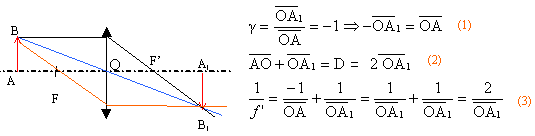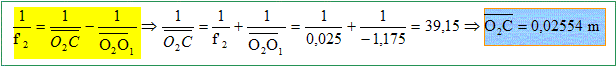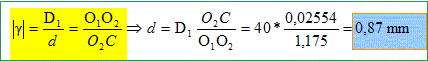Lunette astronomique d'amateur bac S Polynésie 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

Cet exercice traite d'une lunette astronomique construite avec deux lentilles dont les caractéristiques sont : Objectif L1 : diamètre D1 = 40 mm ; distance focale f'1 = 1,15 m Oculaire L2 : diamètre D2 = 15 mm ; distance focale f'2 = 25 mm. Vérification des distances focales. Avec l'objectif il cherche l'image du soleil sur un écran. Quand il obtient une image nette, petite et très lumineuse, il mesure la distance séparant l'objectif de l'écran. Quelle doit être cette valeur ? Justifier. L'image d'un objet situé à l'infini se trouve dans le plan focal image de la lentille. Ecrire la formule de conjugaison : On mesure donc 1,15 m. La méthode précédente ne lui semble pas suffisamment précise pour vérifier la valeur très petite de f'2 aussi préfère t-il utiliser une autre méthode, dite de Silbermann. Il place un objet AB au zéro d'un banc d'optique et perpendiculaire à celui-ci. Il déplace l'oculaire et un écran de façon à obtenir une image A'B' renversée et de même grandeur que l'objet AB. Les points A et A' sont sur l'axe optique de l'oculaire. Il mesure AA' =D= 10,0 cm. Faire la construction graphique correspondante. Tracer deux rayons remarquables issus de B permettant d'obtenir B' et placer les foyers F2 et F'2 de l'oculaire.   la relation (1) traduit le grandissement: le signe moins indique que l'objet et l'image sont de sens contraire. relation (2) : la distance objet image est notée D relation (3) : formule de conjugaison des lentilles pour conclure il suffit de remplacer OA1 par ½D, puis de prendre l'inverse des rapports égaux d'où f ' = D/4. A partir de ce schéma trouver la relation entre AA' = D et f'2 ( aucune démonstration n'est demandée). La valeur trouvée est-elle conforme à l'indication du constructeur ? f ' = D/4 = 10,0/4 = 2,50 cm, en accord avec l'indication du constructeur Grossissement de la lunette. Le foyer image de l'objectif et le foyer objet de l'oculaire sont confondus : la lunette est afocale. Il observe un objet AB considéré à l'infini et perpendiculaire à l'axe optique en A. Le diamètre apparent de l'objet est noté a.   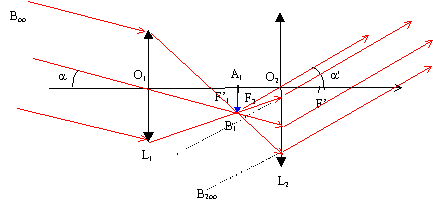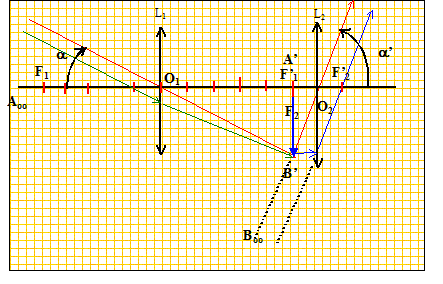Construire l'image A1B1 de AB donnée par l'objectif. Où se forme l'image définitive A'B' ? Justifier. Tracer le rayon émergent de l'oculaire correspondant au rayon issu de B et passant par le centre optique O1 de l'objectif. Un rayon issu de B et passant par le centre optique O1de la lentille n'est pas dévié. B1 est à l'intersection de ce rayon et du plan focal image de L1. L'image définitive A'B' donnée par l'oculaire (L2) est à l'infini car A1B1 ( objet pour l'oxculaire ) est dans le plan focal objet de l'oculaire. Une autre construction : Le grossissement de la lunette est donnée par la relation : G = a' / a. a' est l'angle sous lequel on voit l'image A'B' à travers l'instrument. Les angles étant petits, exprimés en radians, on peut confondre l'angle avec sa tangente. Indiquer a' sur le schéma et exprimer le grossissement en fonction de f'1 et f'2 puis le calculer. Dans le triangle rectangle F2O1B1 : tan a = A1B1 / O1A1 = A1B1 /f'1soit a voisin A1B1 /f'1. Dans le triangle rectangle F2O2B1 : tan a' = A1B1 / O2A1 = A1B1 /f'2soit a' voisin A1B1 /f'2. le grossissement a pour expression G=a' / a = f'1 / f'2= 115 / 2,5 =46. Le grossissement précédent est bien adapté à l'observation de la lune ou des anneaux de saturne. Pour observer le ciel profond ( galaxies, nébuleuses ), l'astronome utilise un grossissement inférieur. Pour cela, sans changer d'objectif, utilise t-il un oculaire de distance focale supérieure ou inférieure à 25 mm ? Justifier. G= f'1 / f'2 : f'1 étant inchangé, si f'2 augmente alors le grossissement G diminue. Cercle oculaire. 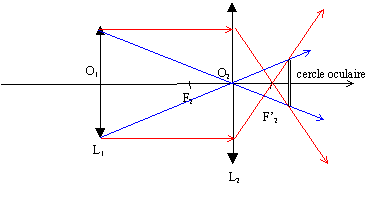Donner la définition du cercle oculaire. Le cercle oculaire est l'image du bord de l'objectif ( lentille circulaire) donnée par l'oculaire. On se place toujours dans le cas d'une lunette afocale. Construire le cercle oculaire sur le schéma. . Calculer la valeur d du diamètre du cercle oculaire.   On note C la position du cercle oculaire. La distance O1O2 vaut f'1+f'2 =1,15+0,025 = 1,175 m. Ecrire la formule de conjugaison ( lentille L2) pour calculer O2C. Utiliser la valeur absolue du grandissement transversal pour le calcul de d : Où l'astronome doit-il placer son oeil et quel doit être le diamètre de sa pupille pour recevoir le maximum de lumière ?  On place l'oeil à la position du cercle oculaire : toute la lumière issue de l'objectif L1 est collectée par l'oeil ; donc l'image A'B' observée est très lumineuse. Le diamètre de la pupille doit être supérieur ou égal au diamètre du cercle oculaire.

retour -menu