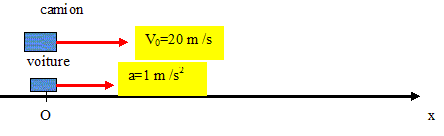Rencontres de mobiles : exercices bac lycée En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

Sur une route rectiligne, un camion roulant à vitesse constante de 72 km/h, passe à la hauteur d'une voiture initialement immobile. L'auto démarre lorsque le camion passe à sa hauteur, avec une accélération constante a = 1 m/s2. A quelle date la voiture ratrappe t-elle le camion ? Quelle est, à cette date, la vitesse de la voiture ? Origine des distances : la voiture immobile en O ; origine des dates : démarrage de la voiture. Les conditions initiales sont les suivantes : Camion : mettre la vitesse en m/s : v= 72/3,6 = 20 m/s. Le mouvement est rectiligne uniforme ; la distance parcourue est : xC= 20 t. Voiture : mouvement retiligne uniformément accéléré. La vitesse est une primitive de l'accélération : v= at + v0 avec une vitesse initiale v0 nulle : v = at = 1*t ; v= t. La position est une primitive de la vitesse xV = ½at2 + x0 avec x0, position initiale, choisie comme origine de l'axe. xV = ½t2. A l'instant de la rencontre : xC=xV ; 20 t = ½t2 ; t = 40 s. 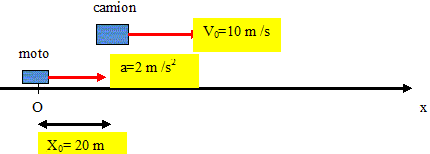Vitesse de la voiture : v = 40 m/s. A une date choisie comme origine, un camion passe davant un motard à l'arrêt. Le camion est animé d'un mouvement rectiligne uniforme v = 36 km/h. Le motard démarre avec une accélération constante a = 2 m/s2 lorsque le camion a parcouru 20 m. A quelle date la moto ratrappe t-elle le camion ? Quelle est, à cette date, la vitesse de la moto ? Origine des distances : la moto immobile en O ; origine des dates : démarrage de la moto. Les conditions initiales sont les suivantes : Camion : mettre la vitesse en m/s : v= 36/3,6 = 10 m/s. Le mouvement est rectiligne uniforme ; la distance parcourue est : xC= 10 t +20. Moto : mouvement retiligne uniformément accéléré. La vitesse est une primitive de l'accélération : v= at + v0 avec une vitesse initiale v0 nulle : v = at = 2*t ; v=2 t. La position est une primitive de la vitesse xM = ½at2 + x0 avec x0, position initiale, choisie comme origine de l'axe. xM = t2. A l'instant de la rencontre : xC=xM ; 10 t +20= t2 ; t2 -10t-20 = 0 ; résoudre D = 102+4*20 =180 ; D ½= 13,41. t =(10+13,41)/2 =11,7 s t ~ 12 s. Le temps ne peut être négatif, seule la solution positive est à retenir. Vitesse de la moto :v = 2*11,7 ; v = 23,4 m/s. 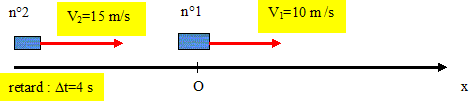Sur une piste rectiligne un premier cycliste passe devant un spectateur à vitesse constante de 36 km/h. Un autre cycliste roulant à vitesse constante de 54 km/h passe davant le spectateur 4 s plus tard. A quelle date la second cycliste ratrappe t-il le premier ? A quelle distance du spectateur ? Origine des distances : le spectateur immobile en O ; origine des dates : le passage du premier cycliste en O. Les conditions initiales sont les suivantes : Cyliste 1 : mettre la vitesse en m/s : v= 36/3,6 = 10 m/s. Le mouvement est rectiligne uniforme ; la distance parcourue est : x1= 10 t. Cycliste 2 : mettre la vitesse en m/s : v= 54/3,6 = 15 m/s. Le mouvement est rectiligne uniforme ; la distance parcourue est : x2= 15 (t-4). A l'instant de la rencontre : x1=x2 ; 10 t = 15(t-4) ; 10t = 15 t-60 ; t = 60/5 ; t= 12 s. 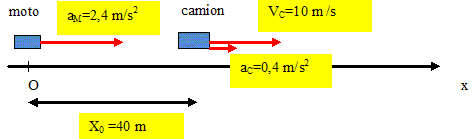Distance du spectateur au lieu de la rencontre : 10t = 10-12 = 120 m. ou bien 15(12-4) = 15*8 = 120 m. A une date choisie comme origine, en un lieu choisi comme origine, une moto démarre avec une accélération constante de 2,4 m/s2. A cette date t=0, un camion situé 40 m en avant de la moto, roulant à vitesse constante de 36 km/h, accélère ( accélération constante de 0,4 m/s2 ). A quelle distance de l'origine, la moto ratrappe t-elle le camion ? Quelles sont, à cette date, les vitesses des véhicules ? Origine des distances : le spectateur immobile en O ; origine des dates : le passage du premier cycliste en O. Les conditions initiales sont les suivantes : Camion : mettre la vitesse en m/s : v= 36/3,6 = 10 m/s. Le mouvement est rectiligne uniformément accéléré avec une vitesse initiale de 10 m/s, avec une position initiale de 40 m/s. La vitesse est une primitive de l'accélération : v= at + v0 ; v=0,4 t +10. La position est une primitive de la vitesse xC = ½at2 +v0t+ x0. xC = 0,2 t2 +10 t+40. Moto : mouvement retiligne uniformément accéléré. La vitesse est une primitive de l'accélération : v= at + v0 avec une vitesse initiale v0 nulle : v = at = 2,4*t ; vM=2,4 t. La position est une primitive de la vitesse xM = ½at2 + x0 avec x0, position initiale, choisie comme origine de l'axe. xM = 1,2t2. A l'instant de la rencontre : xC=xM ; 1,2 t2= 0,2t2+10 t+40 ; t2 -10 t-40 = 0 ; résoudre D =102+4*40 =260 ; D ½= 16,12. t =(10+16,12)/2 =13,06 s t ~ 13,1 s. Le temps ne peut être négatif, seule la solution positive est à retenir. Distance : 1,2*13,062 ~205 m. ou bien : 0,2 *13,062 + 10*13,06 +40 ~205 m. vitesse : vM=2,4 t= 2,4*13,06 =31,3 m/s. vC =0,4 t +10=0,4*13,06+10 =15,2 m/s. 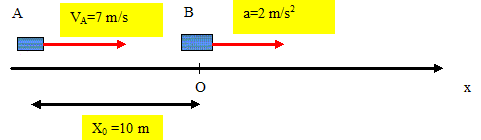Le relais 4x100 m ; on supposera les mouvements rectilignes. A arrive à vitesse constante de 7 m/s ; il passe le ralais à B. Le démarrage de B s'effectue avec une accélération constante de 2 m/s2 lorsque B se trouve 10 m devant A. Quel temps s'écoule entre le démarrage de B et le passage du témoin ? Quelle distance est parcourue par B durant ce temps ? Origine des distances : position initiale de B ; origine des dates : le démarrage de B. Les conditions initiales sont les suivantes : A : le mouvement est rectiligne uniforme ; la distance parcourue est : xA=7 t -10. B : mouvement retiligne uniformément accéléré. La vitesse est une primitive de l'accélération : v= at + v0 avec une vitesse initiale v0 nulle : v = at = 2*t ; v=2 t. La position est une primitive de la vitesse xM = ½at2 + x0 avec x0, position initiale, choisie comme origine de l'axe. xB = t2. A l'instant de la rencontre : xA=xB ; 7t-10= t2 ; t2 -7t+10 = 0 ; résoudre D = 72-4*10 =9 ; D ½= 3. t =(7+3)/2 ; t ~ 5 s. Le temps ne peut être négatif, seule la solution positive est à retenir. Distance parcourue par B en 5 s : 5*5= 25 m.

retour -menu