Le radium bac S Liban 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

1932 : le radium à la mode.... Un examen attentif des dépôts de marque réalisés entre 1927 et 1934 atteste de la "mode radium" qui sévissait alors. Nous avons ainsi recensé une centaine de notices évoquant de près ou de loin, cet élément radioactif. Le Tho-radia revendique haut et fort sa faible teneur en radium : la radioactivité du radium est pratiquement inépuisable. On a calculé qu'elle aurait diminué que de moitié au bout de seize siècles. C'st ce qui fait la différence fondamentale entre une préparation qui contient réellement du radium telle que la crème Tho-radia et les produits qui n'ont été soumis qu'à l'émanation du radium. L'activité de cette émanation disparaît en très peu de temps. D'après Revue d'histoire de la pharmacie" 3è trimestre 2002. Première partie : étude de l'activité du radium 222. Constante radioactive du radium 222 : l = 1,35 10-11 s-1 ; NA = 6,02 1023 mol-1 ; M(Ra) = 226 g/mol. Donner la composition du noyau de radium 22688Ra. 88 protons et 226-88 =138 neutrons. Le radium 226 est un émetteur a. Il conduit au radon de symbole Rn. Ecrire l'équation de la réaction de désintégration et préciser les lois de conservation utilisées. 22688Ra = AZRn +42He. Conservation de la charge : 88=Z+2 ; Z=86. Conservation du nombre de nucléons : 226=A+4 ; A = 222. 22688Ra = 22286Rn +42He. A la date t=0 de fabrication, 100 g de crème Tho-radia contenaient N0 = 3,33 1014 noyaux de radium. Calculer la masse initiale de radium 226 dans 100 g de crème. Citer la phrase du texte d'introduction illustrant ce résultat. n =N0/NA = 3,33 1014 / 6,02 1023 =5,53 10-10 mol m = nM = 5,53 10-10 *226 =1,25 10-7 g. "Le Tho-radia revendique haut et fort sa faible teneur en radium" Donner l'expression de la loi de décroissance du nombre N de radium 226 en fonction du temps. N(t) = N0 exp(-lt). Calculer le pourcentage de noyaux restants à la date t=10 ans. Pourquoi peut-on dire que l'activité due au radium 226 contenu dans la crème ne varie pratiquement pas pendant une période de 10 ans ? 10 ans = 10*365*24*3600 s = 3,154 108 s. lt= 1,35 10-11 *3,154 108 =4,26 10-3. exp(-4,26 10-3) = 0,9958. N= 0,9958 N0 ; N/ N0 = 0,9958 ( 99,6 %) L'activité est proportionnelle au nombre de noyaux présents à la date t ; à 0,4% près ce nombre est pratiquement identique à N0. L'activité du radium 226 est a peu près inchangée au bout de 10 ans. Justifier la phrase du texte "On a calculé qu'elle aurait diminué que de moitié au bout de seize siècles". 16 siecles = 16*100 ans = 16*10*3,154 108 s = 5,046 1010 s. lt= 1,35 10-11 *5,046 1010 =0,681 exp(-0,681) = 0,506. N= 0,506 N0 ; N/ N0 = 0,506 ( 50,6 %) Deuxième partie : étude de l'activité due au radon 222. 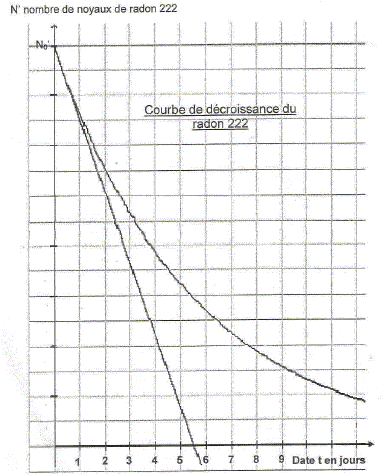Le radon 222 a pour temps de demi-vie 3,8 jours. Le radon 222 produit par la désintégration du radium 226 est lui même radioactif a.   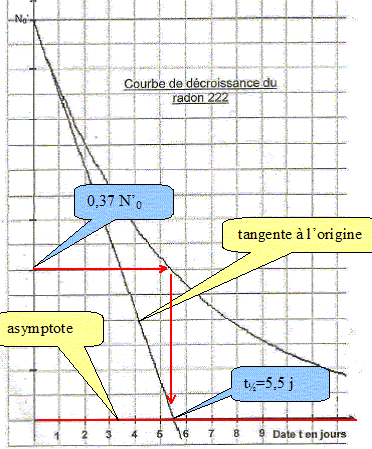Déterminer graphiquement la constante de temps t. Préciser la méthode utilisée. 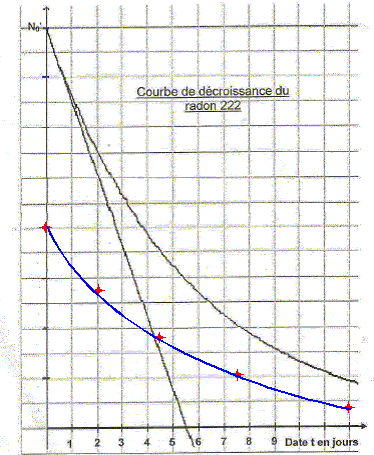Rappeler la définition du temps de demi-vie t½. Etablir son expression en fonction de la constante de temps t puis calculer le temps de demi-vie. La valeur calculée est-elle en accord avec la valeur donnée ? Temps de demi-vie : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés. Loi de décroissance radioactive : N(t) = N0 exp(-lt) = N0 exp(-t/t) . On identifie : t = 1/l. N(t½) = 0,5 N0 = N0 exp(-lt½) ; ln0,5 = -lt½ ; ln2 = lt½ = t½ /t. t½ = t. ln2 = 5,5*0,693 =3,8 jours. ( accord avec la valeur donnée) Construire sur le même graphique, en utilisant les mêmes échelles, la courbe représentant la loi de décroissance du radon 222 pour un nombre initial de noyaux deux fois plus faible.

retour -menu