Mesure de la valeur de la capacité d'un condensateur bac S Inde 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

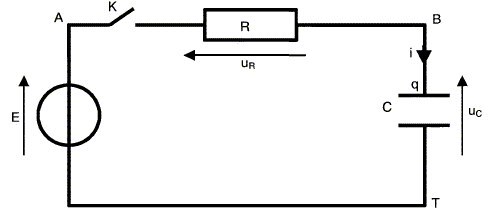
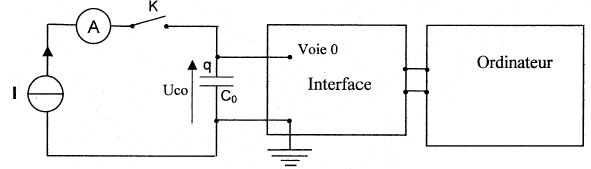
On dispose de deux composants : un conducteur ohmique de résistance R = 150 W et un condensateur de capacité C inconnue. L'objectif de la séance est de déterminer la valeur de C. Pour cela, on choisit d'étudier la charge du condensateur à travers le conducteur ohmique à l'aide d'un générateur de tension de f.e.m. E = 5,1 V. 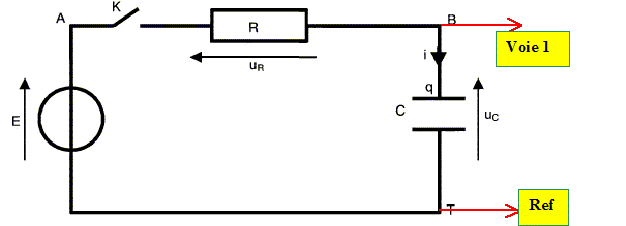On réalise donc le montage schématisé ci-dessous et on utilise par exemple un système d'acquisition informatique Refaire sur la copie le schéma du montage n°1 en indiquant les branchements nécessaires pour suivre l'évolution de la tension uC(t) aux armatures du condensateur en fonction du temps. Les bornes utilisées pour l'acquisition sont notées Voie 1 et Ref (qui sert de masse).  Constante de temps : On suppose le condensateur déchargé. A l'instant t = 0, on ferme l'interrupteur K. On obtient la courbe ci-dessous. Le phénomène observé est caractérisé par une grandeur appelée constante de temps notée t. Que signifie l'expression " phénomène caractérisé par t " ? La constante de temps permet d'estimer la durée de la charge du condensateur : cette durée est voisine de 5 fois la constante de temps. A l'aide de la courbe, estimer l'ordre de grandeur de t sans aucun calcul. Ordre de gransuer de la constante de temps 10 ms ou 10-2 s. Quelle est l'expression de t en fonction des caractéristiques des composants du circuit ? t = RC. Vérifier que l'expression précédente est homogène à un temps. R résistance soit tension / intensité ; C capacité soit charge / tension d'où on déduit : RC charge / intensité or une charge est une intensité fois un temps ; par suite RC a la dimension d'un temps.   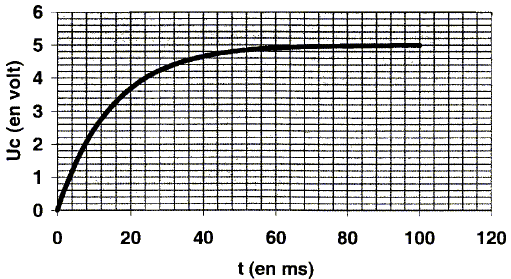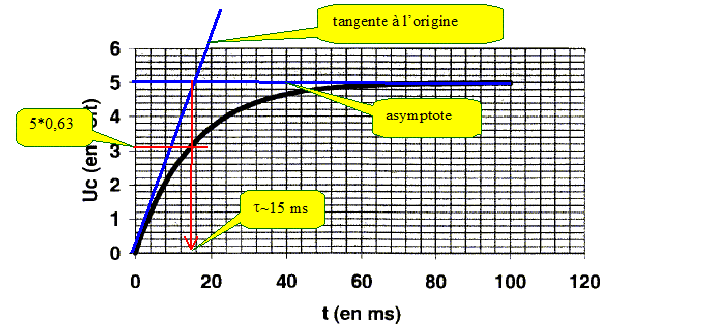Equation différentielle vérifiée par uC(t) : Les conventions de sens et d'orientation pour le courant et les tensions sont indiquées sur le schéma du montage. Ecrire la relation qui existe entre E, uR et uC. Additivité des tensions : uR + uC =E. Exprimer uR en fonction de l'intensité i du courant. uR = R i. Rappeler l'expression de i en fonction de q, charge portée par l'armature reliée au point B du circuit. i = dq/dt. Rappeler l'expression de q en fonction de uc. En déduire celle de i en fonction de uC. q= Cuc ; i = Cduc /dt. En utilisant les résultats précédents montrer que la tension aux armatures du condensateur uC(t) vérifie l'équation différentielle : t duc /dt+uc = E (1) uR + uC =E s'écrit : Ri + uC =E ; RCduc /dt + uC =E ; t duc /dt+uc = E. Propriétés de la fonction uc(t) : Vérifier que uC(t) = E.[1-exp(-t/t ] est solution de l'équation différentielle précédente et satisfait à la condition initiale : t = 0, condensateur déchargé. uC(t) = E.[1-exp(-t/t )] ; duc /dt = E /t exp(-t/t) ; repport dans (1) : t E /t exp(-t/t) +E.[1-exp(-t/t )] = E E exp(-t/t) +E -E exp(-t/t) =E est vérifié quel que soit t. De plus à t=0 : uC(0) =E[1-exp(-0/t )] = E(1-1) = 0, le condensateur est initialement déchargé. Déterminer la valeur du rapport uC/E à la date t = t. uC/E = 1-exp(-1) = 0,63. En utilisant ce résultat et en exploitant la courbe n°1, déterminer la valeur de t puis celle de C. t=15 ms = 15 10-3 s( lecture graphe) ; t =RC avec R=150 W d'où C = 15 10-3 / 150 = 1,0 10-4 F.   Proposer le principe d'au moins une autre mesure de la capacité C. Charge à l'aide d'un générateur de courant : our déterminer la capacité d'un condensateur on réalise la charge à l'aide d'un générateur de courant. Ce générateur débite un courant d'intensité constante I= 0,50 mA. 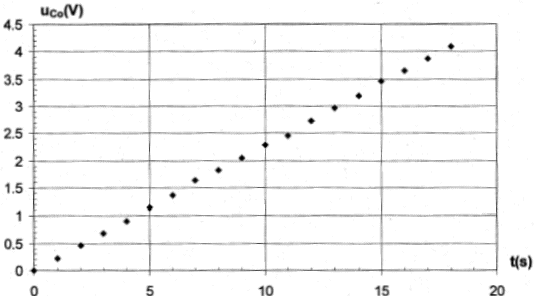La saisie automatique de la tension uc aux bornes du condensateur en fonction du temps est réalisée avec le montage ci-dessous. 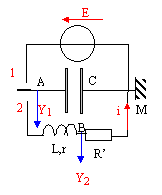On obtient la courbe suivante : q= It ; charge en coulomb, intensité en ampère et temps en seconde uc=q/C0= I/C0t droite de coefficient directeur I/C0. 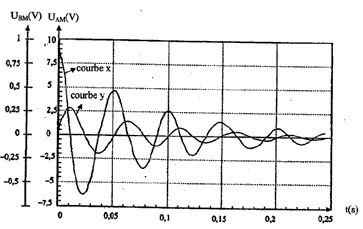Réaliser un oscillateur LC : On réalise le montage suivant comportant un générateur de f.e.m E= 9V et de résistance interne négligeable, un condensateur dont la capacité varie entre 40 et 80 mF, un conducteur ohmique de résistance R'= 5 ohms, une bobine d'inductance L= 1H et de résistance r = 10 ohms. L'interrupteur K est placé en position (1) puis basculé en position (2). L'acquisition des données commence lorsqu'on bascule l'interrupteur K de la position (1) à la position (2).   la détermination de la pseudopériode permet de calculer C.

retour -menu