Quelques propriétés du plutonium 241 bac S Inde 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

Les minerais d'uranium (U) contiennent essentiellement 2 isotopes dans les proportions : 99,3% d'uranium 238 et 0,7% d'uranium 235. Le combustible des centrales nucléaires est un mélange enrichi en uranium 235, c'est-à-dire que la proportion de l'isotope 235 est supérieure à 0,7% (et celle du 238 inférieure à 99,3%). En effet, seuls les noyaux d'uranium 235 sont fissiles, c'est-à-dire susceptibles de subir une fission nucléaire sous l'action d'un neutron. Le plutonium (Pu) n'existe pas dans la nature. Le plutonium 241 est un sous-produit obtenu, dans les réacteurs des centrales nucléaires, à partir de l'uranium 238. On peut en effet schématiser la formation d'un noyau de plutonium 241 par l'équation de réaction nucléaire suivante : 23892U + x n --> 24194Pu + y b- (1) n est le symbole d'un neutron et b- celui d'une particule émise et x et y sont des coefficients entiers à déterminer. Une fois formé, le plutonium 241 est lui-même fissile sous l'action d'un bombardement neutronique. De plus, il est émetteur b- avec une demi-vie de l'ordre d'une dizaine d'années. Définir les termes suivants : noyaux isotopes : deux isotopes ne se différencient que par leur nombres de neutrons ; ils ont le même numéro atomique. fission nucléaire : un noyau "lourd" instable se cassent en deux noyaux plus petits lors du choc avec un neutron ; cette réaction libère beaucoup d'énergie. demi-vie : durée au bout de laquelle l'activité initiale est divisée par 2 ; durée au bout de laquelle le nombres de noyaux radioactifs initiaux et divisé par 2.   Préciser le nombre de masse et le numéro atomique de chacune des deux particules, neutron et b-. 10n : un neutron n'a pas de charge, il est constitué d'un nucléon. b- : 0-1e électron négatif, pas de nucléon. Déterminer les valeurs de x et de y dans l'équation (1). 23892U + x10n --> 24194Pu + y 0-1e Conservation du nombre de la charge :  92+0 = 94-y d'où y=2. Conservation du nombre de nucléons : 238+x=241 d'où x = 3.  23892U + 310n --> 24194Pu + 2 0-1e Détermination des énergies libérées lors de transformations du plutonium 241 : On donne les valeurs numériques qui suivent (u est le symbole de l'unité de masse atomique) : célérité de la lumière dans le vide : c = 3,00.108 m.s-1 charge élémentaire : e = 1,602177.10-19 C unité de masse atomique : 1u = 1,66054.10-27 kg masse du neutron : m(n) = 1,00866 u masse de la particule b - : m(b -) = 0,00055 u masse du noyau de plutonium 241 : m(Pu) = 241,00514 u masse du noyau d'américium 241 : m(Am) = 241,00457 u masse du noyau d'yttrium 98 : m(Y) = 97,90070 u masse du noyau de césium 141 : m(Cs) = 140,79352 u En outre, dans la relation d'équivalence masse énergie, à une masse égale à une unité de masse atomique correspond une énergie égale à 931,494 MeV. Fission du plutonium 241 : Elle se fait selon l'équation : 24194Pu + n -->14155Cs + 9839Y + 3 n (2) Déterminer en MeV la valeur de l'énergie EF libérée lors de la fission d'un noyau de plutonium 241. variation de masse |Dm| = m(Y)+ m(Cs) +2 m(n)- m(Pu = 97,90070 + 140,79352 + 2*1,00866 - 241,00514 |Dm| =0,2936 u. EF =0,2936 *931,494 =273,487 MeV. On dit parfois qu'une réaction de ce type peut donner une réaction en chaîne. Pouvez-vous justifier ce terme ? La réaction (2) libère trois neutrons et en consomme un seul. Ces trois neutrons, lors de chocs avec 3 noyaux de plutonium, conduisent à 3 nouvelles fissions, et ainsi de suite. En une durée très courte, un grand nombre de fissions se produit. Désintégration b - du plutonium 241 : Le plutonium 241 est aussi un émetteur b -. La désintégration se fait selon l'équation : 24194Pu --> 24195Am +b -. (3) Déterminer en MeV la valeur de l'énergie ED libérée lors de la désintégration b - d'un noyau de plutonium 241. variation de masse |Dm| =m(Am) + m(b -)-m(Pu) = 241,00457 +0,55 10-3 -241,00514 = 2 10-5 u ED =2 10-5 *931,494 =1,86299 10-2 MeV~1,9 10-2 MeV. Comparer EF et ED et calculer le rapport EF/ED. ED est négligeable devant EF ; EF/ED = 0,2936 / 2 10-5 = 1,47 104. Les physiciens nucléaires affirment que l'interaction entre nucléons appelée interaction forte est responsable de la fission alors que l'interaction qui s'exerce entre un nucléon comme le neutron et un électron appelée interaction faible est responsable de la désintégration b -. Ces termes vous paraissent-ils justifiés ? L'énergie libérée est d'autant plus forte que l'interaction entre particules est plus forte : la fission mettant en jeu une importante énergie , l'interaction entre nucléons est forte. Par contre la désintégration b - libérant peu d'énergie, l'interaction entre un nucléon et un électron est faible. Étude expérimentale de la radioactivité du Plutonium 241 : Une étude de l'activité d'un échantillon contenant du plutonium 241 permet d'obtenir à différentes dates le rapport du nombre de noyaux non encore désintégrés N à la population initiale N0 de noyaux dans l'échantillon. Les résultats expérimentaux ont été consignés dans le tableau ci-dessous : t (ans) 0 3 6 9 12 N/N0 1 0,85 0,73 0,62 0,53 Rappeler la loi de décroissance radioactive qui représente l'évolution de la population moyenne d'un ensemble de noyaux radioactifs.  N(t) = N0 exp (-lt) avec l t½ = ln 2. l : constante radioactive en an-1 et t½ demi-vie en années. Par une méthode de votre choix, graphique ou numérique, déterminer la valeur du temps de demi-vie t1/2 du plutonium 241. ln(N/N0) = - lt = - ln2/ t½ t ; On trace la courbe d'équation ln(N/N0) = f(t). c'est une droite de coefficient directeur - ln2/ t½. 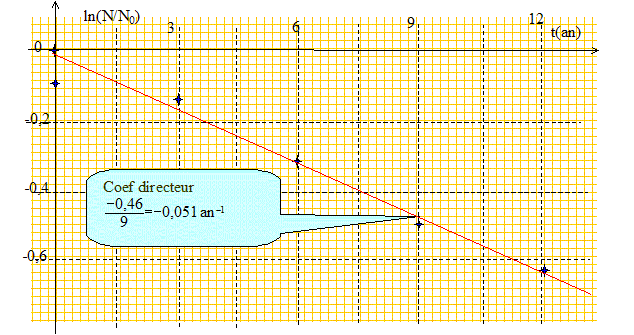t (ans) 0 3 6 9 12 N/N0 1 0,85 0,73 0,62 0,53 ln(N/N0) 0 -0,16 -0,31 -0,48 -0,63 -0,05 = - ln2/ t½ ; t½ = ln2 /0,051= 13,6 ans.

retour -menu