Sciences et sport : énergie mécanique, chute dans l'eau, Euler bac S Nlle Calédonie 03/2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . .

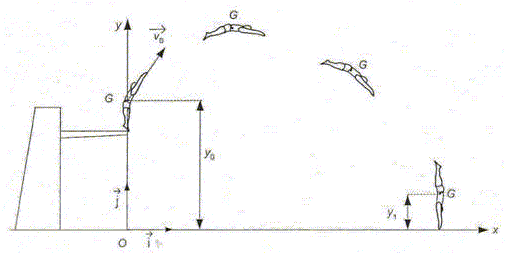
On se propose d'étudier dans un premier temps, le mouvement du centre d'inertie G d'un plongeur de masse m= 70,0 kg lors de son saut et dans une deuxième partie, son évolution dans l'eau. Le mouvement du centre d'inertie du plongeur est étudié dans le repère d'axes (Ox, Oy). Le point O est au niveau de la surface de l'eau et l'altitude du centre d'inertie G du plongeur est notée y. On prendra g = 9,80 m/s2 et on considérera le référentiel galiléen. Etude du saut. Dans toute cette partie on néglige l'action de l'air sur le plongeur au cours de son mouvement et on admet que lors du saut, les mouvements de rotation du plongeur ne perturbent pas le mouvement de son centre d'inertie. On note y0 l'ordonnée du centre d'inertie du plongeur juste avant le saut et v0 sa vitesse initiale. y0 = 4,0 m et v0 = 4,0 m/s. On considère le système {plongeur } dans le champ de pesanteur terrestre. On a représenté ci-dessous l'évolution de l'énergie potentielle de pesanteur du système au cours du temps lors d'une partie de la phase du mouvement étudié. La référence de l'énergie potentielle est prise à la surface de l'eau. Dans ces conditions, l'expression de l'énergie potentielle de pesanteur du système, à l'altitude y, est Epp = mgy. On note tS la date à laquelle l'énergie potentielle de pesanteur est maximale. En utilisant le graphique ci-dessus déterminer l'altitude yS à laquelle se situe le centre d'inertie G du plongeur à l'instant de date tS. yS = EPP max /(mg) = 3,45 103 / (70*9,8) ; yS =5,03 m. Le but de cette question est de déterminer la valeur de la vitesse du centre d'inertie du plongeur au moment où ses mains touchent l'eau. Donner l'expression de l'énergie mécanique du système {plongeur en interaction avec la terre} en fonction de m, g, y et de la valeur de la vitesse v du centre d'inertie du plongeur. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. EM= mgy +½mv2. En justifiant la réponse, dire comment cette énergie évolue au cours du temps. Le plongeur n'est soumis qu'à son poids, les frottements étant négligés. Le poids est une force " conservative" : l'énergie mécanique reste donc constante au cours du temps. Lorsque les mains du plongeur entrent en caontact avec l'eau, le centre d'inertie du plongeur se situe à une hauteur y1 au dessus de l'eau. A cet instant de date t1, donner l'expression, en justifiant la réponse, de l'énergie cinétique du plongeur en fonction de v0, m, g, y0 et y1. Calculer sa valeur si y1 = 1,0 m. Energie mécanique initiale : EM = mgy0 + ½mv02. Energie mécanique finale : EM = mgy1 + Ec fin. Conservation de l'énergie mécanique : mgy0 + ½mv02= mgy1 + Ec fin. Ec fin= m[ g(y0 -y1) +½v02]. Ec fin = 70[9,80 ( 4-1) +0,5 *42]=2618 J ~ 2,6 103 J. En déduire l'expression de la valeur de la vitesse v1 à l'instant de date t1. Calculer sa valeur. Ec fin = ½mv12= 2618 J v1=[2 Ec fin / m]½ = [2*2618 /70]½ =8,6 m/s. 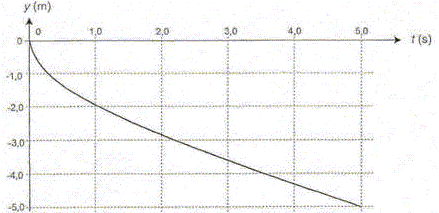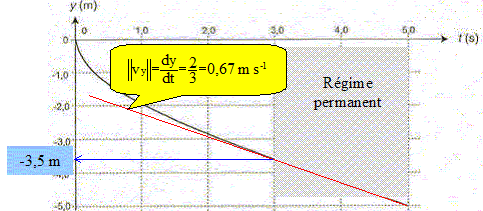Mouvement dans l'eau : Le mouvement du centre d'inertie G du plongeur est considéré comme vertical dans cette partie. La profondeur du bassin dans lequel évolue le plongeur est de 5,0 m. La figure suivante, résulte d'une simulation et représente l'évolution de l'altitude y du centre d'inertie du plongeur au cours du temps. On a pris comme origine des dates l'instant où le centre d'inertie du plongeur atteint la surface de l'eau. Pour pouvoir remonter le plongeur doit redresser son buste. On estime que le plongeur agit activement pour amorcer sa remontée 1,0 s après que son centre d'inertie est atteint la surface de l'eau. De plus, on considère que le centre d'inertie du plongeur se situe toujours à 1 m de ses mains tendues. Au moment où il amorce sa remontée, les mains du plongeur ont-elles atteint le fond du bassin ? Justifier la réponse. D'après le graphe ci-dessus, le centre d'inertie du plongeur à la date t=1 s est à l'altitude y=-2 m. L'extrémité des mains se trouve à l'altitude -3 m et le fond du bassin est à l'altitude -5 m : les mains ne touchent donc pas le fond. On se propose de modéliser le mouvement du centre d'inertie du plongeur dans l'eau s'il n'amorçait pas de remontée. On note V le volume du plongeur et r la masse volumique de l'eau de la piscine. Le plongeur est soumis, entre autres , à une force de frottement fluide dont le sens est opposé à celui de la vitesse v et dont la valeur peut être modélisée par f = kv2 ( où l'on considère k comme une constante). 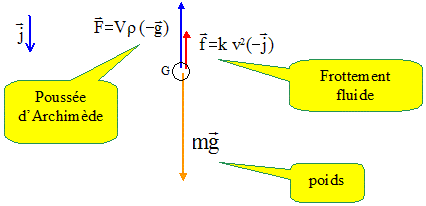Nommer les forces qui s'exercent sur le plongeur. Les représenter sans souci d'échelle. En appliquant la deuxième loi de Newton, montrer que l'équation différentielle qui régit le mouvement du centre d'inertie du plongeur est donnée par : dvy/dt-k/mvy2 +g(1-rV/m)=0 où vy est la composante verticale du vecteur vitesse sur l'axe vetical orienté vers le haut. La deuxiéme loi de Newton s'écrit, suivant un axe vertical orienté vers le haut : -mg + Vrg + kvy2 = mdvy/dt ; mdvy/dt- kvy2 +mg-Vrg =0 Diviser chaque terme par la masse m : dvy/dt- k/m vy2 +g(1-Vr/m) =0. 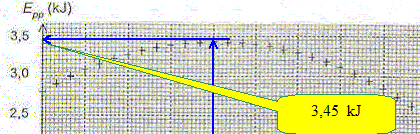En déduire, en la justifiant, l'expression en régime permanent de la valeur vP du vecteur vitesse. En régime permanent le système est pseudo -isolé, les forces se neutralisent. Le mouvement est alors rectiligne uniforme et la valeur de la vitesse est constante. Dans l'expression de l'équation différentielle dvP/dt = 0 d'où : - k/m vP2 +g(1-Vr/m) =0. vP2 =g(m-Vr)/ k ; vP = [g(m-Vr)/ k ]½. Calculer VP. r = 1,00 103 kg m-3 ; V= 6,50 10-2 m3 ; k = 150 kg m-1. VP= [9,8 (70-65) / 150]½ =0,572 m/s. En exploitant la figure ci-dessus dire si le plongeur atteint le régime permanent avant que ses mains ne touchent le fond. Lorsque le régime permanent est atteint, le centre d'inertie est à l'altitude -3,5 m ; l'extrémité des mains se trouve à l'altitude -4,5 m : le fond n'est pas touché. Le régime permanent est atteint avant que les mains ne touchent le fond. 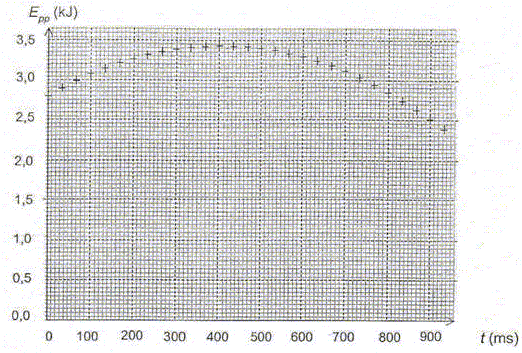Une méthode de résolution numérique possible, la méthode d'Euler permet de calculer de façon approchée la valeur algébrique de la vitesse instantanée verticale vy à différentes dates. On note vy(tn) la valeur algébrique de la vitesse instantanée à la date tn ; on note vy(tn+1) la valeur algébrique de la vitesse instantanée à la date tn+1 =tn +Dt. vy(tn+1) = vy(tn) + ay (tn)Dt. (1) ay : composante verticale de l'accélération ; Dt =1,20 10-2 s est le pas de calcul. Compte tenu des valeurs numériques, l'équation différentielle permet d'obtenir la relation suivante : ay(t)=2,14 vy2(t)-0,700. (2) Compléter le tableau suivant : date en s vy en m/s ay en m/s2 tn = 1,44 10-1 vy(tn) = -2,21 ay(tn)= 9,75 tn+1 = 1,56 10-1 vy(tn+1) = -2,09 ay(tn+1)=8,67 tn+2 = 1,68 10-1 vy(tn+2)=-1,99 ay(tn+2)=7,77 (1) conduit à : vy(tn+1) =-2,21 + 9,75 *1,2 10-2 = -2,09. (2) conduit à : ay(tn+1) =2,14*(-2,09)2 -0,700 = 8,67.

retour -menu