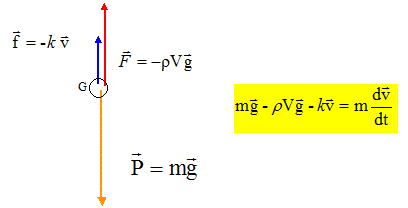Les lois de Newton : chute verticale dans un liquide bac S Asie 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .   Un objet de masse m = 3,80 10-3 kg, de volume V= 2,10 10-6 m3 est lâché sans vitesse initiale dans un liquide de masse volumique r=1240 kg m-3. Sa chute est filmée avec une webcam. le film est numérisé puis analysé par un logiciel adapté. L'intervalle de temps entre chaque image est constant égal à Dt = 0,050 s. Les frottements sur l'objet peuvent être modélisés par une force f opposée au vecteur vitesse et de valeur proportionnelle à la vitesse. Le coefficient de proportionnalité est noté k. On prendra g = 9,8 m/s2. Le mouvement de chute montre deux phases de nature différentes. 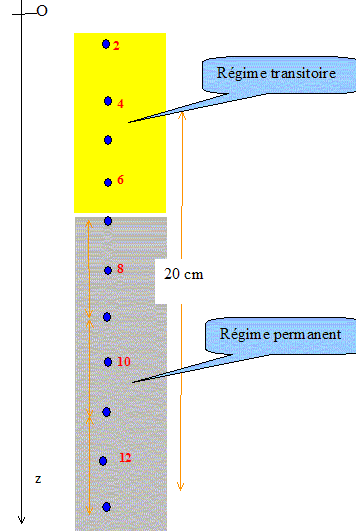Délimiter ces deux phases en précisant approximativement les positions limites de chacune d'elles. Etude de la première phase.  En tenant compte de l'échelle du document, calculer les vitesses en position G3 et G5 puis tracer les vecteurs vitesse en ces positions ( 1 cm <--> 0,20 m/s). Calculer l'accélération a4 au point G4 puis représenter ce vecteur ( échelle 1cm pour 0,50 m/s2). v3 = G2G4/(2Dt) G2G4 ~ 2*0,20/13 ~0,031 m 2Dt = 0,10 s v3 =0,031/0,10 = 0,31 m/s. v5 = G4G6/(2Dt) G4G6 ~ 2,7*0,20/13 ~0,044 m v5 =0,044/0,10 = 0,42 m/s. a4 = (v5 -v3) / (2Dt) a4 =(0,42-0,31)/0,1 = 1,1 m/s2. Etude théorique. Calculer la poussée d'Archimède et montrer qu'elle est de l'ordre de grandeur du poids. Valeur du poids : P= mg = 3,80 10-3 *9,80 =3,72 10-2 N. Valeur de la poussée : poids du volume de fluide déplacé. F =rVg =1240*2,10 10-6*9,8 =2,55 10-2 N Le poids et la poussée sont du même ordre de grandeur : 0,03 N. Représenter les forces sur un schéma sans souci d'échelle.   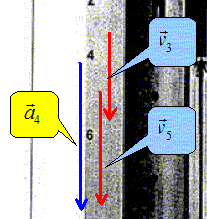Enoncer la loi deNewton qui régit cette première phase. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées au système est égale au produit de la masse du solide par l'accélération de son centre d'inertie G. Calculer la valeur de la force de frottement en position G4. Ecrire la seconde loi de Newton projétée sur l'axe Oz : mg-rVg-f=ma4. f= mg-rVg-ma4 3,72 10-2 -2,55 10-2 -3,80 10-3*1,1 f = 7,5 10-3 N Sachant que la vitesse en position G4 vaut v4 = 0,36 m/s, calculer la valeur du coefficient de frottement k en unité SI. k = f/v : k = 7,5 10-3 / 0,36 =2,1 10-2 kg s-1. Remarque : force : masse * accélération = masse * longueur / temps2 : [force]=MLT-2 ; [vitesse ]=LT-1 ; [force / vitesse]=MT-1. Etude de la seconde phase. Quelle est la nature de cette phase ? 1er point : la valeur de la vitesse est constante 2ème point : le mouvement est rectiligne. 3ème point : énoncé de la première loi de newton : Dans un référentiel galiléen, si un solide est pseudo-isolé, ( somme vectorielle des forces nulle) alors : - le solide est immobile si la vitesse est nulle - le centre d'inertie du solide est animé d'un mouvement rectiligne uniforme et réciproquement.   Déterminer par le calcul la vitesse de l'objet au cours de cette phase. Ecrire que la somme vectorielle des forces est nulle : mg-rVg-k vlimite=0 vlimite=(mg-rVg)/ k (3,72 10-2 -2,55 10-2 ) / 2,1 10-2 vlimite= 0,56 m/s   Retrouver cette vitesse à partir du document en utilisant le point G12. G11G13 ~ 3,5*0,20/13 ~0,054 m 2Dt = 0,10 s v12 =0,054/0,10 = 0,54 m/s.  A 4 % près les deux valeurs concordent.

retour -menu