Aurélie 10/02/07
 

enseignement, concours CAPLP externe 2006 : l'indice de réfraction d'un liquide avec le réfractomètre de Pullfrich.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

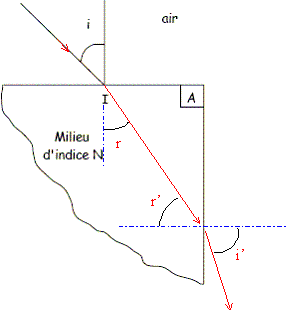
Étude de la déviation d'une lumière monochromatique par un prisme placé dans l'air :

Le rayon laser peut maintenant être orienté grâce à un dispositif adapté de façon à venir frapper la surface d'un prisme en un point I sous une incidence réglable.

Soit un prisme en verre, d'indice de réfraction N pour une longueur d'onde l, d'angle au sommet A = 90°, plongé dans l'air d'indice na.

Marche d'un rayon lumineux monochromatique dans le plan de section principale.

n désignera par i, r, r', i' les angles successifs formés par le rayon lumineux avec les normales aux faces du prisme.
Relations qui existent entre ces angles et l'angle A du prisme :

r+r'=A = 90 soit sin r= cos r' ; loi de Descartes : na sin i = N sin r = N cos r' ; N sin r' = na sin i'.

Montrons qu'il existe, sur la face de sortie, une limite au-delà de laquelle il n’y a plus de rayon émergent :

La plus grande valeur de l'angle i' est 90°, soit sin i' = 1 ; dans ce cas sin r' =na/N avec N >na.

cos2r' = 1 - sin2 r' = 1-(na/N)2 ; cos r' = [1-(na/N)2 ]½.

or sin i = N /na cos r' = N /na[1-(na/N)2 ]½= [(N /na)2-1 ]½. La plus grande valeur possible pour l'angle d'incidence est : i = sin-1[(N /na)2-1 ]½.

Intervention d'un autre milieu :
La face d'entrée du prisme baigne dans un milieu d'indice n (n < N) tandis que la face de sortie baigne dans un milieud'indice na. On fait varier l'angle d'incidence i.

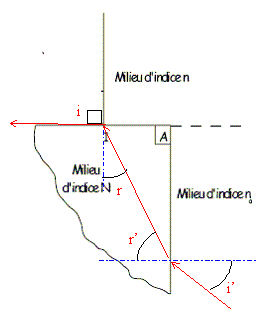
Pour quelle valeur de i' atteint-on la réfraction limite sur la face d'entrée du prisme ?

On affectera l'indice l aux angles correspondant à cette situation.

r1+r'1=A = 90 soit sin r'1 = cos r1 ;

loi de Descartes : na sin i'1 =N sin r'1 = N cos r1

et n sin i1 = N sin r1 = n ; sin r1 = n/N

or cos2r 1 = 1 - sin2 r1 = 1-(n/N)2 ; cos r1 = [1-(n/N)2 ]½.

or na sin i'1 =N cos r1 ; na sin i'1 =N [1-(n/N)2 ]½ =[N2-n2 ]½

n2a sin2 i'1 =N2-n2 ; n2 = N2- n2a sin2 i'1
Une goutte de liquide, d'indice n, est posée sur la face d'entrée du prisme.

Calcul de l'indice n avec : N = 1,6480 ; na = 1,0003 ; i1 = 43°45'.

n2 = N2- n2a sin2 i'1 = 1,6482-(1,0003 sin 43,75)2 =2,2374 ; n = 1,4958.
Sensibilité :

La sensibilité de l'appareil est telle que deux liquides pourront être différenciés par mesure de l'indice, à condition que la variation de l'angle i'l entre les deux

mesures soit au moins égale à une minute d'angle : Di'l = 1'.

Il s'agit de savoir si l'appareil pourra différencier l'o-xylène, le m-xylène et le p-xylène, d'indices respectifs no, nm et np.

Expression de la variation Dn de l'indice de réfraction, en fonction de Di'l .

n2 = N2- n2a sin2 i'1 ;

2 n dn = -2n2a sin i'1cos i'1 di'1 = -½n2a sin (2 i'1) di'1.

dn = -½n2a sin (2 i'1) di'1 / [N2- n2a sin2 i'1 ]½.

Dn= -½n2a sin (2 i'1) / [N2- n2a sin2 i'1 ]½Di'l .

Calcul de Dn :

Dn = -0,5 *1,00032 *sin ( 2*43,75) / [1,6482-(1,0003 sin 43,75)2]½ Di'l .

Dn = -0,334 Di'l avec Di'l = 1/60 degré = 1/60*3,14/180 =2,9 10-4 radian.

Dn = -0,334*2,9 10-4 = 9,7 10-5.

On différencier les 3 produits.

Données : no = 1,5053 ; nm = 1,4972 ; np = 1,4959.
 

retour -menu