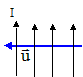|
Lancement d'une fusée ; dipôles RC et RLC : résonance ; solénoïde examen d'accès aux études de kinésithérapie 2002 ( durée : 2h 40) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||||||
| .
. |
|||||||||
|
|||||||||
|
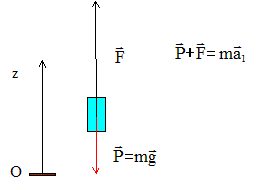
Problème 1 : lancement d'une fusée : ( 8 points ) Un club d'amateurs a construit une petite fusée de masse M = 200 kg. Lors du lancement, le moteur exerce une force de poussée F verticale vers le haut pendant une durée Dt = 10 s, puis le moteur s'arrête et la fusée continue sur sa lancée avant de retomber. On suppose que la trajectoire suit une ligne verticale. Le mouvement est étudié dans le référentiel terrestre supposé galiléen de repère Oz. Dans tout l'exercice, on supposera que la masse de la fusée reste constante et que l'intensité du champ de pesanteur vaut g = 9,8 m.s-2. On suppose dans un premier temps que les frottements sont négligeables.
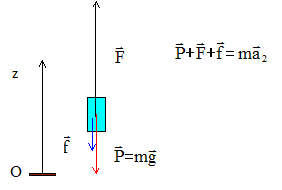
En réalité, les
frottements de l'air ne sont pas
négligeables et se ramènent, tout
au long du mouvement, à une force d'intensité
constante f = 100 N, opposée au mouvement. La force
de poussée F garde la même intensité
constante qu'à la question 1) et s'exerce toujours
pendant 10 s avant que le moteur ne s'arrête. Calculer
l'altitude Z'1 atteinte par la fusée
lorsque le moteur s'arrête.
a1 = F/m-g = constante Pendant la phase de lancement (t<10 s) le mouvement du centre d'inertie de la fusée est uniformément accéléré. La vitesse est une primitive de
l'accélération : v = a1 t F= m(a1+g) = 200(9,8+2,78) ;
F= 2,5 103
N. L'altitude est une primitive de la vitesse : Z= ½a1t2 ; Z1= 0,5*2,78*100 = 139 m ( réponse 1,4 102 m) Après l'arrêt du moteur, le mouvement de la fusée est rectiligne uniformément retardé. ( a'1 = -g= -9,8 m/s²) Altitude maximale, notée Z2, atteinte par la fusée : Ecrire le théorème de l'énergie cinétique entre les altitudes Z1 et Z2 : Travail résistant du poids : -mg(Z2 -Z1 ) variation de l'énergie cinétique : 0-½mv12. ½mv12=mg(Z2
-Z1 ) ; Z2 -Z1
=v12/(2g) = 27,782/19,6
=39,4 m ; Z2 178m ( réponse
1,8 102 m
)
Altitude Z'1 atteinte par la fusée lorsque le moteur s'arrête. Z'1= 0,5*2,2*100 = 110 m ( réponse 1,1 102 m)
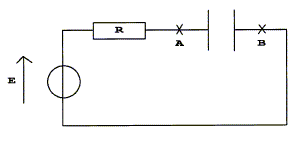
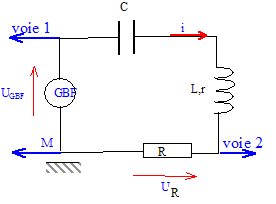
Problème 2 : condensateur et bobine inductive : ( 8 points ) On dispose d'un condensateur et d'une bobine dont on se propose de déterminer respectivement la capacité C, l'inductance L, et l'énergie qu'ils emmagasinent. Partie A : Détermination de la capacité C d'un condensateur. A l'aide d'un générateur de tension continue E, d'un interrupteur K et d'un conducteur ohmique de résistance R, on réalise le montage suivant :
Comme dans la partie A, on visualise sur l'écran d'un ordinateur, la tension aux bornes du générateur basse fréquence (uGBF) et du conducteur ohmique de résistance R (uR) . On réalise le montage suivant avec la bobine L, de résistance r, le condensateur C, et la résistance R en série avec le GBF.
Partie C : Etude énergétique à la résonance. On se place à la résonance, on choisit L = 10 mH et C = 1,1 µF ; R = 1000 W. On a mesuré : - la valeur maximale de la tension aux bornes de R, URmax = 3,8 V - la valeur maximale de la tension aux bornes du condensateur UCmax = 0,36 V.
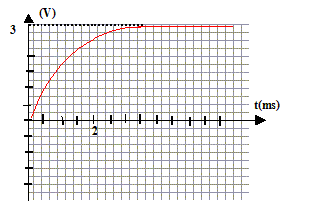
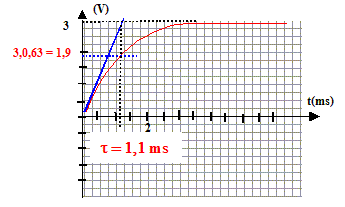
Détermination de la capacité C d'un condensateur. Le phénomène mis en évidence est la charge d'un condensateur à travers un résistor. Détermination du produit RC, constante de temps du circuit :
Intersection de l'asymptote horizontale avec la tangente à l'origine : l'abscisse de ce point donne RC. ou bien à t =RC, la tension aux bornes du condensateur vaut 63% de sa valeur maximale. L'abscisse de ce point donne RC. RC= 1,1 ms = 1,1 10-3 s. Sachant que R = 1000 W, valeur de C : 1,1 10-3 / 1000 = 1,1 10-6 F = 1,1 mF.
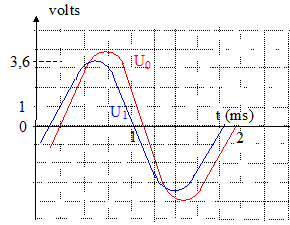
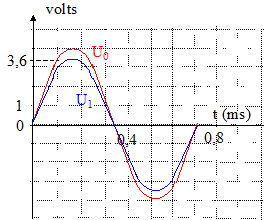
Détermination de l'inductance L de la bobine. On a relevé les enregistrements. Les enregistrements reproduits sur les figures ont été obtenus dans les mêmes conditions d'expérimentation, à l'exception d'un paramètre qui a varié. La fréquence du GBF a changé ( dans l'un des cas la période vaut 0,7 ms, dans l'autre elle vaut 1,8 ms) Les tensions relevées sont repérées par u0 et u1. La valeur maximale de la tension aux bornes du résistor ne peut pas être supérieure à la valeur maximale de la tension aux bornes du GBF : donc u1 correspond à la tension uR aux bornes du résistor. La tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles : u1 est l'image de l'intensité au facteur R près. u0 est la tension aux bornes du dipôle RLC. Lorsque u0 et u1 sont en phase (courbes non décalées) on observe le phénomène de résonance d'intensité. La fréquence du GBF vaut : 1/0,7 10-3 =
1429 Hz ( réponse 1,4
103 Hz) Valeur de L sachant que C = 1,1 µF : L= 1/(Cw02) =1/( 1,1 10-6* 89742)=0,011 H. Etude énergétique à la résonance. On se place à la résonance, on choisit L = 10 mH et C = 1,1 µF ; R = 1000 W. On a mesuré : - la valeur maximale de la tension aux bornes de R, URmax = 3,8 V - la valeur maximale de la tension aux bornes du condensateur UCmax = 0,36 V. Valeur maximale de l'intensité i (t) du courant : Imax = URmax /R = 3,8/1000 = 3,8 10-3 A. Energie maximale emmagasinée par la bobine : ½LI2max = 0,5*0,01*(3,8 10-3)2 = 7,2 10-8 J. Energie maximale emmagasinée par le condensateur : ½CU2max = 0,5*1,1 10-6*(0,36)2 = 7,2 10-8 J.
Problème 3 : solénoïde : ( 4 points ) Vous devez répondre, par Vrai ou par Faux, à chacune des 4 affirmations suivantes, en justifiant votre réponse. Soit un solénoïde, de longueur L, comportant N = 50 spires. Le diamètre du solénoïde est suffisamment petit devant sa longueur pour qu'on puisse le considérer comme infiniment long. Le solénoïde est parcouru par un courant d'intensité I = 2,5 A dont le sens est indiqué sur le schéma. Données : - Perméabilité magnétique du vide : m0 = 4 p 10-7 S.I. - On prendra p = 3,14.
|
|||||||||
|
|
|||||||||
|
|