|
Densimètre ; loi de Poiseuille ; équation Bernoulli d'après LSTA 1ère année. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||
| .
. |
|||
|
|||
|
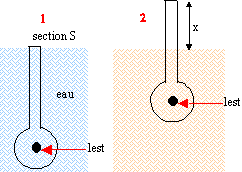
V : volume total du densimètre ; S : section de la partie cylindrique. Plongé dans l'eau de masse volumique re, il affleure (1); par contre dans un liquide de masse volumique r >re, il occupe la position (2). |
|||
|
|
|||
Le densimètre est en équilibre sous l'action de deux forces opposées, son poids P=mg et la poussée d'Archimède F, de valeur égale au poids de volume de liquide déplacé. Volume de liquide déplacé = volume du réservoir + volume de la tige cylindrique de hauteur h V= V1+pd2/4 h Poussée F= Vgr ; poids P=mg d'où : Vr = m ; V1+pd2/4 h = m/r ; pd2/4 h = m/r - V1 h = 4(m/r - V1) / (pd2) avec m = 5,11 10-2 kg ; V1=4,8 10-5 m3 ; d = 4 10-3 m h = 4(5,11 10-2/ 1000-4,8 10-5) / (3,14 *16 10-6)=0,247 m.
|
|||
|
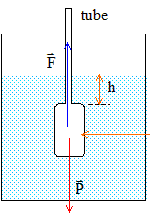
Une perte de pression Dp apparaît entre deux points distants d'une longueur l d’une canalisation de rayon r, dans laquelle un fluide circule à la vitesse moyenne v , avec un débit volumique qv constant. La viscosité h est constante à pression et température fixées.
Dans le cas d'un fluide parfait, la
viscosité est nulle et en conséquence
D
p est nulle.
Calcul de Dp : Dp =rgDh = 900*10*0,3 = 2,7 103 Pa. Calcul de la viscosité : h= pr4Dp / (8lqv) avec r= 4 10-3 m ; l= 0,65 m ; qv =4 10-6 m3/s ; Dp =2,7 103 Pa. h= 3,14 ( 4 10-3)4*2,7 103/(8*0,65*4 10-6 )=1,04 10-1 Pa s. vitesse moyenne du fluide : débit ( m3/s) = section (m2) * vitesse m/s) v = qv / (pr2)=4 10-6 / (3,14*1,6 10-5) =8,0 10-2 m/s. nombre de Reynolds NR = 2r r v/h : NR =2*900*4 10-3*8 10-2/0,104 = 5,5. Le nombre de Reynolds est faible : l'écoulement est laminaire.
|
|||
|
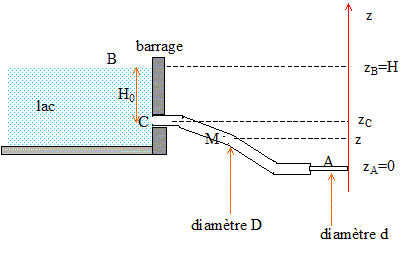
Le niveau du lac est pratiquement constant ; la vitesse de l'eau en B est pratiquement nulle. Notations : p0 : pression atmosphérique ; r : masse volumique de l'eau. Expression de la vitesse de l'eau en A : Relation de Bernoulli : p/r + gz + ½v² = constante. g représente la valeur du champ de pesanteur terrestre. Cette relation peut être applicable à tout le fluide si : le fluide est incompressible (r constant), "parfait" ( viscosité nulle), en régime permanent et sans transfert de chaleur. Appliquer cette relation entre A et B : état A : pression p0 ( à la sortie du petit tube, l'eau est en contact avec l'air ); altitude nulle, vitesse vA. état B : pression p0 ; altitude H, vitesse nulle. d'où p0 /r +gH +0 = p0 /r + 0 + ½v²A ; vA = (2gH)½. vitesse et pression en M : le débit volumique est constant : débit ( m3/s) = section (m2) * vitesse m/s) pD²/4 vM = pd²/4 vA ; D² vM = d² vA ; vM =(d/D)2vA. Appliquer la relation de Bernoulli entre B et M : état M : pression pM ; altitude z, vitesse vM. état B : pression p0 ; altitude H, vitesse nulle. d'où p0 /r +gH +0 = pM /r +gz + ½v²M . p0 +gHr = pM +gz r + ½rv²M . pM = p0 +g(H-z)r- ½rv²M ; pM = p0 +g(H-z)r- ½r(d/D)4v²A. pression en C : altitude du point C : zC= H-H0 ; d'où H-zC= H0 ; pC = p0 +gH0r- ½r(d/D)4v²A. Or H0 < H-z en conséquence pC < pM valeur minimale de d telle que la pression dans la conduite soit toujours supérieure à une valeur pmini : La pression est la plus faible en C d'où : pmini > p0 +gH0r- ½r(d/D)4v²A. pmini - p0 > gH0r- ½r(d/D)4v²A avec v²A = 2gH pmini - p0 > gH0r- rgH(d/D)4 ; (pmini - p0) / (rgH ) >H0 / H - (d/D)4 ; (d/D)4 > H0 / H + (pmini - p0) / (rgH ) d > D[H0 / H + (pmini - p0) / (rgH )]1/4.
|
|||
|
|