Aurélie 31/01/07
 

termes spectraux ; couplage spin orbite ( Russel Sanders)

concours ingénieur police scientifique 2003

Google

Un électron de la dernière couche de l'atome de calcium est excité vers un niveau 4p.

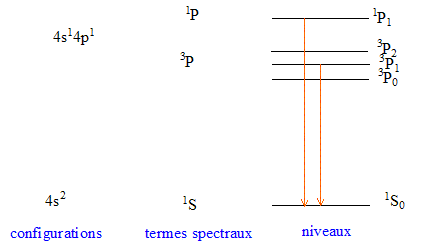
Configuration électronique de cet état excité et termes spectraux correspondant à celle-ci :

Ca ( Z = 20) : 1s2 2s2 2p6 3s2 3p6 4s2 dans l'état fondamental

1s2 2s2 2p6 3s2 3p6 4s1 4p1 dans un état excité

Le mouvement orbital de l'électron donne naissance à un champ magnétique interne, champ qui peut interagir avec l'aimantation (moment magnétique) intrinsèque associée au spin du même électron. On appelle cette interaction (faible), couplage spin-orbite.

Dans l'état fondamental 4s2 :

L'un des électrons a pour nombre quantique : l1=0 et s1 = ½ ; l'autre a pour nombre quantique : l2=0 et s2 = -½ ;

Composition du moment cinétique total : |l1-l2|<= L<= l1+l2 ; d'où L = 0

Composition du spin total : |s1-s2|<= S<= s1+s2 ; d'où S = 0

Il y a un seul couple (L,S) : L=S=0 non dégénéré ( L+1)(2S+1) = 1

couplage spin orbite : |L+S|<=J <= L+S ; d'où J=0

Le terme spectral correspondant à l'état fondamental 4s2 est : 1S0.

Dans l'état excité 4s1 4p1

L'un des électrons a pour nombre quantique : l1=0 et s1 = ½ ; l'autre a pour nombre quantique : l2=1 et s2 =½ ;

Composition du moment cinétique total : |l1-l2|<= L<= l1+l2 ; d'où L = 1

Composition du spin total : |s1-s2|<= S<= s1+s2 ; d'où S = 0 ; 1

Il y a deux couples (L,S) : L=1 ; S=0 et L=1 et S=1

couplage spin orbite : L=1 ; S=0 donne J= 1 ; L=1 et S=1 donne J= 2, 1, 0

Les termes spectraux correspondants à l'état excitél 4s1 4p1 sont : 2S+1PJ soit 1P1 (L=1; S=0; J=1 )

3P0 (L=1; S=1; J=0 ) ; 3P1 (L=1; S=1; J=1 ) ; 3P2 (L=1; S=1; J=2 ).

Seules certaines transitions sont permises ; les règles de sélection sont : DL=+1 ou -1 ; DJ=+1 ou -1 ou 0 ( mais la transition J=0 vers J=0 n'est pas possible)
Un électron 4 p de la dernière couche de l'atome de germanium [Ar] 4s 2 3d 10 4p 2 est excité vers un niveau 4d.

Configuration électronique de cet état excité 4p14d1 et termes spectraux correspondant à celle-ci :

Dans l'état excité 4p1 4d1

L'un des électrons a pour nombre quantique : l1=1 et s1 = ½ ; l'autre a pour nombre quantique : l2=2 et s2 =½ ;

Composition du moment cinétique total : |l1-l2|<= L<= l1+l2 ; d'où L = 1, 2 ou 3

Composition du spin total : |s1-s2|<= S<= s1+s2 ; d'où S = 0 ; 1

Il y a six couples (L,S) :
couple (L,S)
terme spectral

2S+1G
dégénérescence :

2S+1
niveau 2S+1GJ
L=1 ; S=0 ; couplage spin orbite : |L-S| <= J<= L+S soit J= 1
1P
3
1P1
L=1 ; S=1 donne J= 2, 1, 0
3P
9
3P2 ;3P1 ; 3P0
L=2 ; S=0 donne J= 2
1D
3
1D2
L=2 ; S=1 donne J= 3, 2, 1
3D
9
3D3 ; 3D2 ; 3D1
L=3 ; S=0 donne J=3
1F
3
1F3
L=3 ; S=1 donne J= 4, 3, 2
3F
9
3F4 ; 3F3 ; 3F2

 

retour -menu