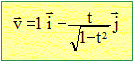|
Cinématique : vitesse , accélération, base de Frenet, projectile. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||
| .
. |
|||||
|
|||||
|
Les équations horaires d'un mouvement plan sont : x(t)=t ; y(t)=(1-t2)½. Quelle est la nature de la trajectoire ? Eliminer le temps y2 =1-t2 et t2 = x2. d'où : y2 =1-x2 ; x2 + y2 =1. cercle de centre O ( origine du repère) et de rayon R= 1. Déterminer le vecteur vitesse et sa valeur : Le vecteur vitesse est la dérivée par rapport au temps du vecteur position. Le vecteur vitesse est tangent à la trajectoire et a le sens du mouvement. dx/dt = vx = 1. dy/dt = vy = ½ (-2t)(1-t2)-½ ; vy = -t (1-t2)-½
valeur v2 =
vx2 +
vy2 v2 = 1
+t2/(1-t2) = 1 /
(1-t2). v = 1 /
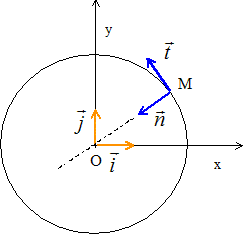
(1-t2)½. En déduire les composantes normale et tangentielle du vecteur accélération : Dans la base de Frenet associée au point M :
Accélération normale dirigée suivant le vecteur unitaire n de la base de Frenet : valeur ( norme) aN= v2/ R avec R= 1. aN= 1 / (1-t2). Accélération tangentielle suivant le vecteur unitaire t de la base de Frenet : aT= dv/dt avec v = 1 / (1-t2)½. aT = t (1-t2)-3/2. Déterminer les composantes cartésiennes du vecteur accélération : Le vecteur accélération est la dérivée par rapport au temps du vecteur vitesse. dx/dt = vx = 1 donc dvx/dt = 0. dy/dt = vy = ½ (-2t)(1-t2)-½ ; vy = -t (1-t2)-½ On pose u = -t soit u' = -1 et w= (1-t2)-½ soit w' = t (1-t2)-3/2 dvy/dt = u'w + uw' = -(1-t2)-½ -t2(1-t2)-3/2 dvy/dt = - (1-t2)-3/2.
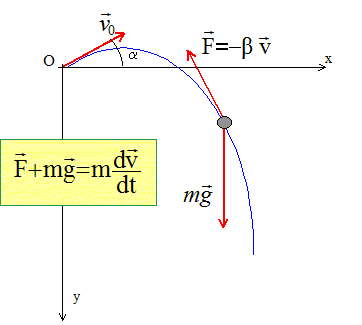
On lance un projectile avec une vitesse initiale de module v0 faisant un angle a avec l'horizontale. Le projectile est soumis à une force de résistance de l'air, colinéaire au vecteur vitesse mais de sens contraire, de norme bv, avec b positif. Expression du vecteur vitesse.
On note vx et vy les composantes du vecteur vitesse. Projection sur l'axe Ox : -bvx +0 = m dvx/dt. dvx/dt + b/m vx =0. Solution de cette équation différentielle : vx = A exp(-b/m t). à t=0, vx = v0 cos a d'où A = v0 cos a vx = v0 cos a exp(-b/m t). Projection sur l'axe Oy : -bvy +mg = m dvy/dt. dvy/dt + b/m vy =g. (1) Solution de cette équation différentielle sans second membre: vy = B exp(-b/m t). Solution particulière de (1) : vy= mg/b ( régime permanent, vitesse limite constante ). Solution générale de (1) : vy = B exp(-b/m t)+ mg/b. à t=0, vy = v0 sin a d'où B = v0 sin a - mg/b vy = (v0 sin a - mg/b ) exp(-b/m t) + mg/b.
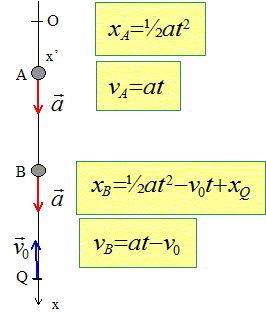
Soit x'x un axe vertical dirigé vers le bas. Un mobile ponctuel A part d'un point O de x'x, choisi comme origine, sans vitesse initiale ; il décrit la demi droite Ox avec une accélération constante, vecteur a. Au même instant un mobile B est lancé avec une vitesse v0 dirigée vers le haut d'un point Q de x'x. B est animé d'un monvement d'accélération constant vecteur a' = vecteur a. A et B se croisent en M. A l'instant de leur rencontre les deux mobiles ont des vitesses de même valeur. Calculer les normes OQ et OM. Au point M : ½at2-v0t+xQ=½at2. xQ= v0t. Les vitesses en M ont même norme mais sont de sens contraire : at = -at + v0 soit : t = ½v0/a. d'où xQ = ½v02/a. xM = ½at2 ; xM =0,125 v02/a. |
|||||
|
|
|||||
|
|