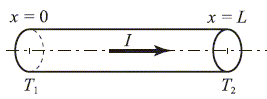Aurélie 30/01/07
 

enseignement, physique, agrégation interne 2006 : effet Joule et effet Thomson dans un fil conducteur

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

Sir William Thonson ( Lord Kelvin) découvre en 1852 l'effet maintenant appelé Joule-Kelvin ou effet Thomson. Il résulte du passage du courant électrique dans un conducteur où règne un gradient de température. La puissance Thomson absorbée lors du passage d'un courant d'intensité I dans un tronçon de fil dont les extrémités sont portées à des températures différant de dT s'écrit : dPT= hIdT. Le coefficient h s'exprime en J K-1. Il est appelé coefficient de Thomson du conducteur. Cet effet dépend du sens de passage du courant. On convient de compter h positif si le passage du courant dans le sens des températures croissante s'accompagne d'une absorption d'énergie. C'est le cas du cuivre.

On néglige dans un premier temps l'effet Thomson pour se consacrer à l'effet Joule.

Une barre conductrice de cuivre calorifugée de longueur L, de section s, de conductivité électrique g et de conductivité thermique l, est parcourue par un courant d'intensité I uniformément réparti. Les températures imposées aux extrémités sont T1(x=0) et T2 ( x=L). La masse volumique du cuivre est r. Sa capacité calorifique massique est c. La température T(x,t) est identique en tout point de la section d'abscisse x.

Loi de conduction de Fourier pour la conduction de l'énergie thermique :

Les vecteurs sont écrits en gras et en bleu.

F= - l grad T

Le transfert spontané de chaleur s'effectue de la région où la température est la plus élevée vers la région où la température est la plus basse.

La densité de flux de chaleur F est proportionnelle au gradient de température grad T .

l : conductivité thermique W m-1 K-1. T (température ( K)

Puissance Joule fournie à la barre entre les sections d'abscisse x et x+dx :

d PJ = d RI2 avec dR = 1/(g S)dx ; d PJ =I2/(gS) dx.

Bilan énergétique pour une section comprise entre x et x+dx :

flux thermique de conduction : - S dF

Volume du cuivre compris entre les sections d'abscisse x et x+dx : S dx ; masse de cuivre : Srdx ; capacité thermique : S c rdx

énergie correspondante : S c rdx dT ; puissance : S c rdx dT/dt

Bilan : - S dF + I2/(gS) dx = S c rdx dT/dt ; - S dF/dx + I2/(gS) = S c r dT/dt (1)

Equation différentielle vérifiée par d T/dx :

Loi de Fourier : F = - l dT/dx ; dF/dx = - l d2T/dx2 repport dans (1) :

Sl d2T/dx2+ I2/(gS) = S c r dT/dt ; d2T/dx2+ I2/(glS2) = c r/ l dT/dt (2)
On considère le régime permanent T(x) ; T(x) ne dépend pas du temps dT/dt =0

(2) s'écrit : d 2T/d x2+ I2/(glS2) = 0

d 2T/dx2 = - I2/(glS2) ; d 2T/dx2 = - K I2 avec K = 1/(glS2)

Calcul de K si l= 400 W m-1 K-1 ; g = 6 107 S m-1 ; S = 2 mm2 = 2 10-6 m2.

K= 1/[ 6 107 * 400 * 4 10-12) = 10,42 K A-2 m-2.

Expression de T(x) :

d 2T/dx2 = - K I2 ; d 2T = - K I2dx2

première intégration : dT= - K I2dx + A avec A une constante.

seconde intégration : T(x) = - ½K I2 x2+ Ax + B avec B une constante.

T(x=0) = T1 = B

T(x=L) = T2 = - ½K I2L2+ AL+T1 soit A= ½K I2L+(T2 -T1)/L.

T(x) = - ½K I2 x2+ ½K I2L +(T2 -T1)x/L + T1.

Valeur maximale de T(x) :

dT/dx = - K I2x + ½K I2L2 +(T2 -T1)/L

dT/dx =0 soit x = ½L +(T2 -T1)/(LK I2).

de plus x doit être compris entre 0 et L ; d'où la condition sur l'intensité I :

½L +(T2 -T1)/(LK I2) <L ; (T2 -T1)/(LK I2) <½ L ;

LK I2 > 2(T2 -T1) / L ; I2 >2(T2 -T1) /(K L2).

On suppose que T2 -T1 = 100 K. ; L= 1,00 m

Calcul de la valeur minimale de l'intensité conduisant à un maximum de température entre les extrémités du fil :

I2 >2(T2 -T1) /(K L2) ; I2 > 200 / 10,42 ; I2 >19,20 ; I > 4,38 A.

On prend en compte l'effet Thomson. On se place en régime permanent dans la situation où le courant I et les températures T2 etT1 satisfont les conditions I >4,38 A et T2 >T1. Le courant I circule dans le sens des températures croissantes.

Equation différentielle à laquelle obéit la distribution de température :

- S dF + I2/(gS) dx - dPT =0 avec F = -l dT/dx ; dPT = hIdT

S l dx d 2T/dx2 + I2/(gS) dx - hIdT =0

d 2T/dx2 + I2/(glS2) - hI / (S l ) dT/dx =0.

Valeur de I, notée I2 pour laquelle on obtient un gradient de température uniforme dT/dx = (T2-T1)/L = constante :

d 2T/dx2 =0 soit I22/(glS2) = hI2 / (S l ) dT/dx ;

I2/(gS) = h dT/dx ; I2= hgSdT/dx ; I2=hgS(T2-T1)/L.

Calcul de I2 si h = 2,2 10-6 V K-1 :

I2 = 2,2 10-6 * 6 107 * 2 10-6 *100 = 0,0264 A = 26,4 mA.
 

retour -menu