Aurélie 05/02/07
 

chimie : cinétique d'un échange de ligands ; concours Agrégation interne 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

Etude cinétique de la réaction : (suivi par spectrophotométrie )

[Co(H2O)(NH3)5]3++ SCN- --->[Co(SCN)(NH3)5]2++ H2O

on note C1 : [Co(H2O)(NH3)5]3+ et C2 : [Co(SCN)(NH3)5]2+

La longueur d'onde utilisée est 497 nm, pour laquelle la différence des coefficients d'extintion molaire des deux complexes est maximale.

La longueur de la cuve utlisée est l.

La première série de mesures est réalisée à 70°C avec [ C1]0=3,30 10-3 mol/L et [SCN-]0=0,400 mol/L

absorbance A
0,228
0,266
0,302
0,337
0,379
0,400
0,441
0,461
0,482
0,620
t(min)
49
67,5
88
111
140
160
202
227,5
262,5
infini
Ordre global apparent :

vitese de la réaction : v = k [ C1]a[SCN-]b

[SCN-] >> [ C1]0 ; [SCN-] peut être considéré comme constant.

vitesse de la réaction dans ces conditions : v = k' [ C1]a avec k'= k [SCN-]b

Expression de l'absorbance en fonction de e 1, e2, l, [ C1], [ C2] :

A= (e 1[ C1] + e2[ C2] ) l. (1)

Expression de l'absorbance en fonction de e 1, e2, l, [ C1], Aoo :
avancement volumique (mol/L)
C1
+SCN-
=C2
+H2O
initial
0
[ C1]0
[SCN-]0=constante
0
solvant en grand exès
en cours
x
[ C1]0 -x
x
final
xfin
[ C1]0 -xfin
xfin
[ C1]0 -xfin = 0 ; xfin =[ C1]0

de plus Aoo = e2 l [ C2]fin = e2 lxfin =e2 l[ C1]0 soit [ C1]0 =Aoo /(e2 l)

et [ C1]= [ C1]0 -x = [ C1]0 -[ C2] ; [ C2] = [ C1]0 -[ C1] = Aoo /(e2 l)-[ C1]

repport dans (1) : A= (e 1[ C1] + e2( Aoo /(e2 l)-[ C1]) ) l.

A= (e 1-e2)[ C1]l + Aoo.

[ C1] =(A- Aoo) / ((e 1-e2)l) ; d[ C1]/dt = 1/ ((e 1-e2)l) dA/dt

v = -d[ C1]/dt = k'(A- Aoo)a/ ((e 1-e2)l)a

-1/ ((e 1-e2)l) dA/dt = k'(A- Aoo)a/ ((e 1-e2)l)a

dA/dt =- k'(A- Aoo)a/ ((e 1-e2)l)a-1

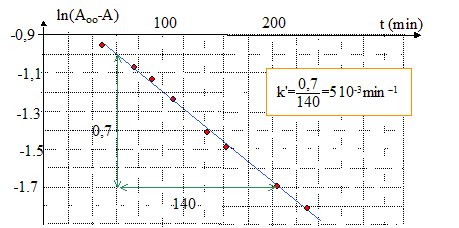
Vérifions que l'ordre global apparent vaut 1 :

dA/dt =- k'(A- Aoo) ; dA /(A- Aoo) = -k' dt

par intégration : ln(A- Aoo) = -k't + constante ; à t=0 , A=A0.

d'où : ln[(A0- Aoo) /(A- Aoo)] = k't ; ln[(Aoo- A0) /(Aoo- A)] = k't ;

ln (Aoo-A) = -k't +ln (Aoo-A0)

tracer le graphe ln (Aoo-A) = f(t) ; droite de pente k'.

absorbance A
0,228
0,266
0,302
0,337
0,379
0,400
0,441
0,461
0,482
0,620
t(min)
49
67,5
88
111
140
160
202
227,5
262,5
infini
Aoo -A
0,392
0,354
0,318
0,283
0,241
0,22
0,179
0,159
0,138


ln(Aoo-A)
-0,936
-1,038
-1,146
-1,262
-1,422
-1,514
-1,72
-1,84
-1,98



D'autres séries de mesures ont été effectuées dans les mêmes conditions de température à partir des solutions suivantes préparées dans des fioles jaugées de 100 mL et complétées à 100 mL avec de l'eau déminéralisée.
solution
1
2
3
4
5
6
volume thiocyanate de sodium à 2,00 mol/L (mL)
10,0
20,0
25,0
30,0
35,0
40,0
volume solution acide perchlorique à 0,5 mol/L (mL)
2
volume solution perchlorate de sodium à 2 mol/L (mL)
30
20
15
10
5
0
quantité de matière C1 (mol)
3,30 10-4
constante de vitesse k' ( s-1)
4,23 10-5
8,3 10-5
1,02 10-4
1,16 10-4
1,44 10-4
1,58 10-4
L'acide perchlorique est un acide fort, il n'interagit pas dans la réaction mais permet par l'intermédiaire des protons libérés, d'éviter la dissociation des complexes. La série de mesures exploitées précédemment correspond à la solution 2.

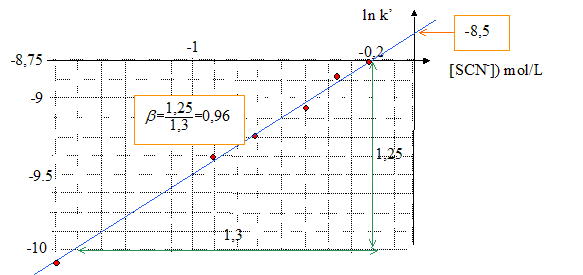
Rôle de la solution de perchlorate de sodium : elle garde constante la force ionique de chaque solution.

Ordre partiel de la réaction par rapport à SCN- :

k'= k [SCN-]b ; ln k' = ln k + b ln [SCN-]

tracer la courbe ln k' = f([SCN-]) ; droite de pente b et d'ordonnée à l'origine ln k.

solution
1
2
3
4
5
6
volume thiocyanate de sodium à 2,00 mol/L (mL)
10,0
20,0
25,0
30,0
35,0
40,0
[SCN-] (mol/L)
2*10/100 = 0,2
2*20/100 = 0,4
0,5
0,6
0,7
0,8
ln [SCN-]
-1,61
-0,92
-0,69
-0,51
-0,36
-0.22
constante de vitesse k' ( s-1)
4,23 10-5
8,3 10-5
1,02 10-4
1,16 10-4
1,44 10-4
1,58 10-4
ln k'
-10,1
-9,4
-9,19
-9,06
-8,84
-8,75

ln k = -8,5 d'où k = 2 10-4 s-1 L mol-1.
 

retour -menu