Aurélie 15/01/07
 

Agrégation interne 2006 : rayonnement de l'électron dans le modèle de Thomson

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

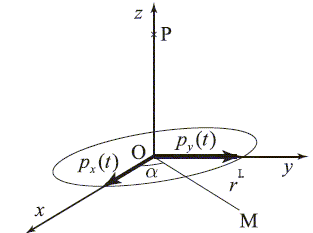
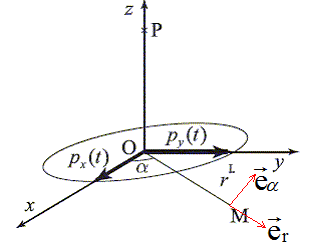
Les vecteurs sont écrits en gras et en bleu.

L'atome d'hydrogène est considéré comme un double dipôle oscillant appliqué en O : px=p0cos(wt) ; py=p0sin(wt). Il rayonne un champ électromagnétique.

Shématisons les composantes du champ E associé aux deux dipôles en un point M du plan (Oxy). M est repéré par les coordonnées polaires r et a.

Pour r=OM >> l=2pc/w, le champ magnétique rayonné en M par un dipôle oscillant, de moment dipolaire px(t) = p0 cos (wt) ex, placé en un point O est tel que :

Ex= -w2 sina/( 4pe0rc2) p0 cos(w(t-r/c))ea.

Le champ magnétique rayonné en M par un dipôle oscillant, de moment dipolaire py(t) = p0 sin (wt) ey, placé en un point O est tel que :

Ey= -w2 cosa/( 4pe0rc2) p0 sin(w(t-r/c))(-ea) = w2 cosa/( 4pe0rc2) p0 sin(w(t-r/c))ea.

par suite : E=[ -w2 sina/( 4pe0rc2) p0 cos(w(t-r/c)) + w2 cosa/( 4pe0rc2) p0 sin(w(t-r/c))]ea.

E=w2p0 /( 4pe0rc2) [ - sina cos(w(t-r/c)) +cosa sin(w(t-r/c))]ea.

E=w2p0 /( 4pe0rc2) sin[w(t-r/c)-a]ea.

Le champ électrique E garde une orientation constante de vecteur unitaire ea : l'onde dans le plan Oxy est donc polarisée rectilignement.

Composantes du champ E en un point P( OP=r) de l'axe Oz de l'orbite :

Le champ magnétique rayonné en P par un dipôle oscillant, de moment dipolaire px(t) = p0 ex, placé en un point O est tel que :

Ex= -w2 /( 4pe0rc2) p0 cos(w(t-r/c))(-ex) = w2 /( 4pe0rc2) p0 cos(w(t-r/c))ex.

Le champ magnétique rayonné en P par un dipôle oscillant, de moment dipolaire py(t) = p0 ey, placé en un point O est tel que :

Ey= -w2 /( 4pe0rc2) p0 sin(w(t-r/c))(-ey) = w2 /( 4pe0rc2) p0 sin(w(t-r/c))ey.

Les composantes Exet Eyont la même amplitude ; elles sont décalées de ½p : l'onde en P est donc polarisée circulairement.
On admet que l'énergie moyenne rayonnée par unité de temps PR est celle de deux dipôles d'amplitude p0, de pulsation w. PR = w4 p20 /( 6pe0c3) ;

Cette énergie correspond à une diminution PR= - dEm/dt de l'énergie mécanique Em de l'oscillateur constitué par l'électron.

Em = m w2p20 / e2. La diminution de Em entraîne celle de p0 et en conséquence celle du rayon a de l'orbite.

On admet que la pulsation reste inchangée et que p0 décroît suffisamment lentement dans le temps pour que le mouvement reste circulaire durant des intervalles de temps grand devant T=2p/w correspondant à la période propre de la radiation considérée de l'hydrogène ( l= 434,1 nm)

Dans ces conditions - dEm/dt=Em/t, t étant la constante de temps.

PR = w4 p20 /( 6pe0c3) ; Em = m w2p20 / e2.

PR= - dEm/dt = Em/t ; w4 p20 /( 6pe0c3) = m w2p20 / (e2t)

soit t = 6mp e0c3 / (e2w2)

- dEm/dt = Em/t ; d(lnEm)= -dt /t

par intégration : ln Em = -t /t + constante notée E0 ou bien Em = E0 exp(-t /t)

A.N : w = 4,34 1015 rad/s ; m =9,1 10-31 kg ; e = 1,6 10-19 C ; e0c2= 7,96 105 ; c = 3 108 m/s.

t = 6mp e0c3 / (e2w2) = 6*9,1 10-31 *3,14* 7,96 105*3 108 /(1,6 10-19 * 4,34 1015)2 =8,5 10-9 s.

or T = 2p/w = 6,28 / 4,34 1015 = 1,45 10-15 s.

L'hypothèse t >> T est bien vérifiée. Le modèle de Thomson, par contre, n'est pas correct.
 

retour -menu