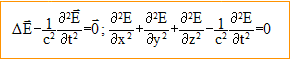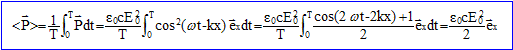|
Agrégation interne 2006 : champ électromagnétique dans le vide. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|
| .
. |
|
|
|
|
On donne les équations de Maxwell que doivent vérifier respectivement le vecteur champ électrique E et le vecteur champ magnétique B en notant r la densité volumique de charge et j le vecteur densité de courant. (e0 et µ0 étant respectivement la permittivité et la perméabilité du vide : µ0 e0 c2 = 1)
On repère tout point M de l'espace à l'aide d'un repère ( O, ex, ey, ez) Montrons qu'une onde plane rectiligne E= E0 cos(wt-kx)ey peut se propager dans le vide ; E0 est l'amplitude constante. Elle doit vérifier l'équation de propagation, obtenue à partir des équations de Maxwell :
d2Ey/dy2 = d2Ey/dz2 = 0 ; dEy/dx = kE0 sin(wt-kx) ; d2Ey/dx2 = -k2E0 cos(wt-kx) = - k2Ey. dEy/dt = -wE0 sin(wt-kx) ; d2Ey/dt2 =-w2E0 cos(wt-kx) = -w2Ey. par suite : - k2Ey- (-w2/ c2E y) 0 ; relation vérifiée si k = w/c. Direction de propagation : l'axe x'x Valeur de la norme du vecteur d'onde
k : k = w/c
B=E0
/ c cos(wt-kx)ez
;
B,
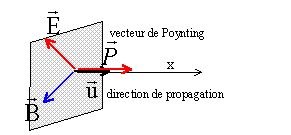
E,
ex
forment un trièdre direct ( figure ci-dessous)
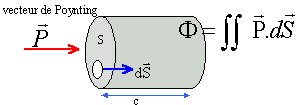
P = E^B / m0 avec B = u^ E /c et E = cB^ u d'où : P = cB²/ m0 u = ce0 E² u = ce0E20 cos2(wt-kx)u L'énergie se propage dans le sens de l'onde à la vitesse c. Le flux du vecteur de Poynting à travers une surface S est égale à l'énergie contenue dans un cylindre de section S et de longueur c ( énergie transmise à travers une surface par unité de temps)
F = PS=ce0 E²S Son unité est W m-2. Valeur moyenne de <P> sur une période en fonction de E0, e0 et c, vitesse de la lumière dans le vide.
Un faisceau lase polarisé rectilignement est assimilable à une onde plane de section 1 mm². Pour une puissance transportée P0 = 100 mW, calcul de l'amplitude du champ électrique correspondant : P0 = ½e0cE02S ; E02 =2P0 / ( e0cS) avec e0 =1/(m0c2) E02 =2P0 m0c / S avec P0 =0,1 W ; m0= 4 p 10-7 ; c = 3,00 108 m/s ; S= 10-6 m². E02 =2*0,1*4
p
10-7 *3,00 108 / 10-6 =7,54
107 ; E0
=8,7
103 V/m.
Cette onde est dite "circulaire ":
l'amplitude E0 est
constante ; le vecteur
E
tourne à vitesse constante w
autour de l'axe Ox.
B = ex ^ E /c B =E0 /c [cos(wt-kx)ex ^ey+ sin(wt-kx)ex ^ez ] B =E0 /c [cos(wt-kx)ez + sin(wt-kx)(-ey) ] P = E^B / m0 P =E20 / (cm0)[ cos(wt-kx)ey + sin(wt-kx)ez]^[cos(wt-kx)ez + sin(wt-kx)(-ey)] P =E20 / (cm0)[cos2(wt-kx)ex+sin2(wt-kx)ex] =E20 / (cm0)ex =e0cE02ex Le vecteur de Poynting
P
est constant : il ne
dépend ni de x, ni du
temps.
|
|
|
|
|
|
|