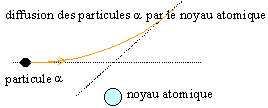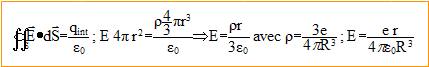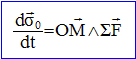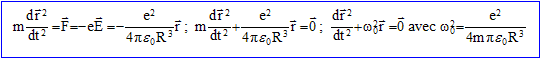|
Agrégation interne 2006 : modèle atomique de Thomson |
|
| .
. |
|
|
|
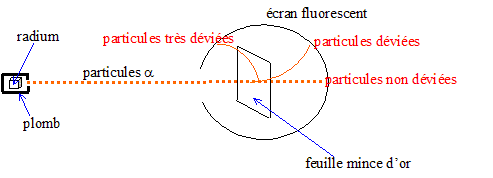
Ce modèle n'était pas capable d'expliquer les raies du spectre d'émission de l'hydrogène. Il ne précisait pas la nature de la matière constituant la sphère positive, ni la densité de charge. Rutherford, Schrodinger, Bohr firent évoluer le modèle de l'atome. Expérience de Rutherford :
La plupart des particules ne sont pas déviées ; un petit nombre est très déviée : donc, la charge positive de l'atome est concentrée dans un volume de l'ordre de 10-13 m, appelé noyau, et non pas répartie sur une sphère de rayon 10-8 m. Rutherford estima la taille du noyau d'or (Z=79) en déterminant la distance minimale d'approche R0 des particules a correspondant à un angle de diffusion de 180°.
Valeur de R0 si l'énergie cinétique initiale des particules a est de 7,7 MeV : L'énergie initiale des particules a est sous forme cinétique : ½mv² = 7,7 MeV = 7,7 106 eV =7,7 106 * 1,6 10-19 J =1,23 10-12 J Lors de leur passage au plus près du noyau d'or, l'énergie de la particule a ( charge +2e) est sous forme potentielle : 2Ze2/(4pe0R0). L'énergie mécanique se conserve : 2Ze2/(4pe0R0) =1,23 10-12 . R0 = 2Ze2/(4pe0 *1,23 10-12 ) avec Z= 79 ; e = 1,6 10-19 C et 1/(4pe0 ) = 9 109. R0 =2*79*(1,6 10-19)2 * 9 109 /(1,23 10-12 ) = 3 10-14 m.
Mouvement de l'électron dans l'atome de Thomson : L'atome d'hydrogène n'est soumis à aucune action extérieure. On s'intéresse à l'oscillation libre de l'électron par rapport à la sphère de centre O. On admet que l'électron ne perd pas d'énergie par rayonnement. Les vecteurs sont écrits en gras et en bleu. A l'instant t, l'électron est en M tel que OM= r = r er ( r<= R). L'électron de l'atome d'hydrogène se déplace dans le champ électrostatique du proton représenté par une distribution volumique de charges uniforme de rayon R. densité de charge volumique : r = charge / volume de la sphère de rayon R ; r = e / (4/3pR3) = 3e/ (4pR3). L'électron n'est soumis qu'au champ électrique crée par une distribution volumique représentant le proton. Ce champ est radial. Appliquons le théorème de Gauss à une sphère de centre O (centre de l'atome), de rayon r <R.
A l'instant t=0, l'électron est écarté de sa position d'équilibre par une perturbation quelconque. Nature du mouvement : Il est alors soumis à la force centrale F=-e E = -e2/(4pe0R3) r . Le référentiel d'étude étant galiléen : La dérivée par rapport au temps du moment
cinétique du point matériel M par rapport au
point fixe O est égal au moment, par rapport à
ce point, de la somme vectorielle des forces agissant sur le
point matériel M . Or OM et F sont colinéaires ; le produit vectoriel OM ^ F est nul ; en conséquence le moment cinétique s0 est constant : le mouvement est plan, perpendiculaire à s0. Dans un référentiel supposé galiléen, lié au proton, le pricipe fondamental appliqué au proton s'écrit :
On retrouve l'équation d'un oscillateur harmonique de pulsation w0. La nature de la trajectoire ( droite, cercle, ellipse ) dépend des conditions initiales concernant la position et la vitesse.
Calcul de R pour laquelle la pulsation w0 correspond à la fréquence n0 d'une des raies du spectre de Lyman de l'atome d'hydrogène ( l0 =121,8 nm) : n0 =c/ l0 = 3 108 / 121,8 10-9 =2,67 1014 Hz. w0 = 2pn0 =6,28 *2,67 1014 =1,68 1015 rad/s. w20 =2,82 1030 ; e = 1,6 10-19 C ; m = 9,1 10-31 kg ; 1/(4pe0 ) = 9 109. w20 =e2/(4pe0 mR3) ; R3=e2/(4pe0 mw20 ) R3=(1,6 10-19 )2 9 109 /(9,1 10-31 *2,82 1030 )= 9 10-29 ; R =4,5 10-10 m. Cette valeur est supérieure à celle trouvée dans l'expérience de Rutherford ; elle est de l'ordre de grandeur du rayon de l'atome. On admet que l'électron décrit une trajectoire circulaire de rayon a dans le plan Oxy perpendiculaire à un axe Oz dans le sens direct. Latome possède alors un moment dipolaire p= -e r équivalent à deux dipoles élémentaires px(t) et py(t). Expression de ces dipoles : p = -e a er = p0er avec p0 = - ea px(t) = p0 cos (w0t) ; py(t) = p0 sin (w0t) Expression de l'énergie mécanique Em de l'oscillateur constitué par l'électron en fonction de p0, w0, m et e : Em = ½mv2 + ½e2/(4pe0R3) a2 ; or v =w0 a d'où : Em = ½[ m w20 a2+ e2/(4pe0R3) a2 ] ; or w20 =e2/(4pe0 mR3) d'où : |
|
|
|
|
|
|