Aurélie 20/12/06
 

Agrégation 2006 : thermodynamique des milieux magnétiques ; refroidissement par désaimantation adiabatique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

Les variables naturelles utilisées seront : la température T, l’aimantation M et l’excitation magnétique H. Les grandeurs vectorielles auront toutes la même direction Oz, c’est pourquoi nous n’utiliserons que des grandeurs scalaires, composantes de ces vecteurs selon Oz.

On utilise préférentiellement la variable H plutôt que le champ magnétique B :

L’excitation magnétique H dépend des courants dans les bobinages ; l'induction magnétique B dépend également du matériau.

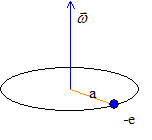
Moment magnétique L et moment cinétique atomique mB:

Soit un modèle classique d’atome à un électron en mouvement orbital circulaire autour du noyau.

moment cinétique L de l’électron : L= me a2w ; moment magnétique mB (magnéton de Bohr) associé à ce mouvement : mB= -½ea2w ;

mB= -e/(2me) L avec me, masse de l'électron. mB= e/(2me) h, h quantum de moment cinétique.

mB =1,6 10-19 / 2* 9,11 10-31) *1,05 10-34 =9,2 10-24 A m2.

cas d'un atome alcalin :

L'électron externe appartient à une orbitale s pour laquelle L=0 ; le moment cinétique de spin est égal à + ou - ½ ; mB diffère de zéro ( un électron non apparié)

cas d'un atome alcalino-terreux :

Les deux électrons externes appartiennent à une orbitale s pour laquelle L=0 ; le moment cinétique de spin est nul ( 2 électrons appariés ) ; mB =0.

Paramagnétisme à deux niveaux :

Milieu paramagnétique au niveau microscopique : existence de moments magnétiques atomiques susceptibles de s'orienter dans un champ magnétique extérieur.

Ferromagnétique : propriété de certains corps de s'aimanter fortement et de conserver partiellement cette aimantation après disparition du champ extérieur.

Soit une assemblée de moments magnétiques indépendants ne pouvant prendre que deux états de projection selon l’axe Oz : ± mB. La température T est maintenue constante. Un champ extérieur H est imposé. L’énergie d’un dipôle magnétique dans ce champ vaut : Ep =± mBB = ± mBm0H.

 Expressions des probabilités normalisées pour un dipôle d’être dans l’état + mB et – mB :

P+ = A exp[mBm0H / (kT)] ; P- = A exp[-mBm0H / (kT)] ; avec P+ + P- =1

A [exp[mBm0H / (kT)]+exp[-mBm0H / (kT)] ]=1 ; A [2 ch[mBm0H / (kT)]] ;A= 1/[2 ch[mBm0H / (kT)]]

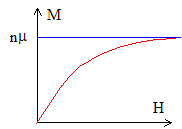
Expression de l’aimantation M(T, H) s’il y a n dipôles par unité de volume :

M(T,H)= nmB(P+ -P-)= nmBA[exp[mBm0H / (kT)]-exp[-mBm0H / (kT)] ] = nmB A[2 sh[mBm0H / (kT)]]

M(T,H)=nmB [2 sh[mBm0H / (kT)]] / [2 ch[mBm0H / (kT)]] = nmB th[mBm0H / (kT)]

Expression de la susceptibilité magnétique cm =M / H du milieu :
saturation du milieu à champ extérieur important ou bien à basse température : cm =nmB

proportionnalité entre M et H à champ extérieur faible ou à haute température :

th[mBm0H / (kT)] proche de : mBm0H / (kT) d'où cm =nm2Bm0 / (kT)

Le milieu a-t-il un comportement linéaire si th[mBm0H / (kT)] peut être assimilé à mBm0H / (kT) ; soit kT >> mBm0H

M= nm2Bm0 / (kT) H

Évaluation de la susceptibilité magnétique cm d’un paramagnétique solide à 300 K si n = 1029 m-3 pour un solide, m0 =4p 10-7 H m-1, mB =9,2 10-24 A m2 , k =1,38 10-23 J K-1:

cm = nm2Bm0 / (kT) = 1029(9,2 10-24)24p 10-7 / (1,38 10-23*300)=2,6 10-3. 

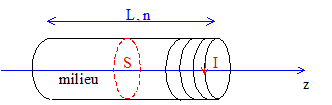
Thermodynamique d’un milieu paramagnétique :

Dans cette partie, l’équation d’état du milieu magnétique supposé linéaire est : M= C/T H (loi de Curie) où C est la constante de Curie.

Le milieu magnétique cylindrique, de section S et de longueur L, est entouré d’un bobinage jointif comportant n spires par mètre, réparties uniformément, parcourues par un courant d’intensité I.

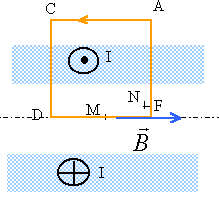
Calcul du champ H dans le milieu en fonction de I, en admettant la nullité de H à l’infini et en négligeant les effets de bord :

le champ magnétique à l'intérieur du solénoide est parallèle à l'axe de la bobine.

Il reste invariant dans une translation parallèle à l'axe z et par rotation autour de cet axe.

On choisit le contour ACDF pour appliquer le théorème d'Ampère.

trajet AC : le champ est nul à l'extérieur du solénoïde

trajet AF et CD : le vecteur champ et trajet sont perpendiculaires: la circulation du champ est nulle

trajet DF : C = H L

intensité des courants enlacés : n L spires sur la longueur L

théorème d'Ampère : C = H L =n I : H = n/L I .

Un contour similaire passant par N donne le même résultat : le champ est donc uniforme à l'intérieur du solénoïde.

On impose une variation élémentaire d’intensité dI.

Une f.e.m induite Einduit= -dF/dt apparaît aux bornes de la bobine pendant la durée de cette variation.

Le travail élémentaire fourni par le générateur au système est alors : dWop = -Einduit Idt = IdF où dF est la variation de flux de B à travers le bobinage.

Travail élémentaire apporté au système par unité de volume en fonction de H et dB :

D'une part H= nI ; I= H/n ; d'autre part F = nLBS ; par suite : d Wop =H L S dB

d Wop par unité de volume : HdB

Or B=m0(H+M) ; dB= m0 (dH+dM) ; HdB= Hm0 (dH+dM) = m0HdH+m0HdM = m0d(½H2)+m0HdM

m0d(½H2) : part d’énergie apportée à la variation du champ dans le vide.

m0HdM : part d’énergie fournie au milieu.

On note s l’entropie par unité de volume.

Les différentielles de l’énergie interne volumique u(s, M) et de l’enthalpie libre généralisée volumique g(T, H) du milieu. sont :

du= dWrév + d Q rév = m0HdM + Tds

g= u-Ts-m0HM soit dg = du-Tds-sdT-m0HdM-m0MdH

dg = m0HdM + Tds-Tds-sdT-m0HdM-m0MdH ; dg = -sdT-m0HdM

g est une fonction d'état ; par suite : [ds/dH]T =m0[dM/dT]H

Expression de la différentielle de s(T, H) pour le milieu considéré en fonction de T et de H.

cH la capacité thermique du milieu à champ H constant.

ds = cH /T dT + [ds/dH]T dH = cH /T dT +m0[dM/dT]H dH

or M= C/T H d'où [dM/dT]H = -CH / T2.

Refroidissement par désaimantation adiabatique :

Une substance paramagnétique à la température T1 et vérifiant la loi de Curie est soumise à un champ H1 : on dit qu’elle est aimantée. Si ensuite le milieu est calorifugé, une désaimantation par diminution du champ à la valeur H2 < H1 conduit à un refroidissement à T2 < T1. Cette désaimantation, effectuée lentement, peut être considérée réversible. Elle permet l’obtention de très basses températures de l’ordre de quelques mK.

Relation entre dT et dH lors d’une telle désaimantation :

désaimantation réversible, adiabatique et isentropique d'où ds = = 0

or ds = cH /T dT-m0CH/ T2dH ; dT = m0C/(cHT )H dH

Stabilité thermique du milieu à H constant :

à l'équilibre thermique, la température du milieu et la température extérieur sont identiques.

hypothèse : T devient supérieure à Textérieur

alors le système échange ( cède) de l'énergie avec l'extérieur ; si cH >0, cet échange d'énergie entraîne une diminution de la température du système. L'équilibre du milieu est stable.

or dT = m0C/(cHT )H dH ; si H diminue ( dH<0) alors dT est négative. La désaimantation s’accompagne d’un refroidissement du milieu.

Aux très basses températures c’est la contribution magnétique qui domine dans l’expression de la capacité thermique, ce qui nous amène à fixer : cH (T, H = 0) = 0. Expression de cH (T, H) :

s est une fonction d'état : ds = cH /T dT-m0CH/ T2dH ;

[dcH/dH]T = -Td (m0CH/ T2) /dT = 2m0CH/ T2

cH = m0CH2/ T2

La désaimantation est effectuée en diminuant le champ d’un facteur 10 : H2 = H1 / 10. La température finale T2 vaut : (T1 = 1 K )

d'une part dT = m0C/(cHT )H dH ; d'autre part cH = m0CH2/ T2

d'où : 1/ T dT = 1/H dH soit d(lnT) = d(lnH) ; H/T = constante

H2 /T2 =H1 /T1 ; T2 =H1 /H2T1 = 0,1 K.

L'aimantation M ne varie pas si H/T = cte ; la terminologie « désaimantation » n'est pas correcte.

retour -menu