Aurélie 08/11/07
 

Mouvement d'un train : accélération, freinage, relevement d'un virage concours kiné EFOM 1999

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

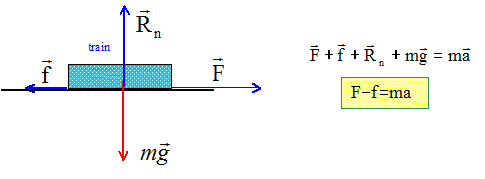
Un train comprend une motrice de masse M=50 t et 5 wagons ; chacun a une masse de 10 t. Au cours du démarrage il atteint la vitesse de 40 m.s-1 en 40 s.

Les forces de frottements représentent 100 N par tonne en mouvement. La voie est rectiligne et horizontale.

Déterminer la force de traction, d'intensite constante, développée par le moteur de la locomotive.

Système : le train ; référentiel terrestre supposé galiléen.

accélération = variation de la vitesse / durée de cette variation

a = 40/40 = 1 m s-2.

Force motrice :

F= f+ma avec m = 100 t = 105 kg et f = 100*100 = 104 N

F= 104 + 105*1 = 1,1 105 N.

Un ressort de constante k=105 N m-1 est placé entre le dernier et l'avant dernier wagon.

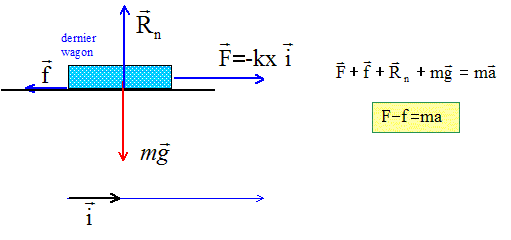
Déterminer l'alongement x de ce ressort au cours de la phase de démarrage étudiée précédemment.

Système : le dernier wagon ; référentiel terrestre supposé galiléen.

m = masse du dernier wagon : m = 10 t = 104 kg

f = 100*10 = 103 N ; a = 1 m s-2.

F= f+ma = 103 + 104 = 1,1 104 N

allongement : x = F/k = 1,1 104 / 105 = 0,11 m = 11 cm.

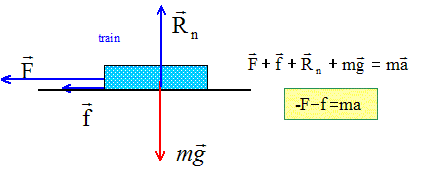
Le train ralentit : le freinage s'exerce sur tous les essieux du convoi à raison de 1900 N par tonne du mouvement. La voie est rectiligne, horizontale.


Déterminer la valeur algébrique de l'accélération au cours de cette nouvelle étape.

Système : le dernier wagon ; référentiel terrestre supposé galiléen.

m = 100 t = 105 kg ; f = 100*100 = 104 N ; F= 100*1900 = 1,9 105 N

a = -(1,9 105 + 104 ) / 105 = - 2 m s-2.
Déterminer l'allongement du ressort placé entre le dernier et l'avant dernier wagon du train.

m = masse du dernier wagon : m = 10 t = 104 kg

f = 100*10 = 103 N ; a = -2 m s-2.

F= f + ma = 103 -2 104 = -1,9 104 N

allongement : x = F/k = -1,9 104 / 105 = -0,19 m = -19 cm.

Le signe moins traduit le fait que le ressort est comprimé.
En négligeant les forces de frottement par rapport aux forces de freinage et en supposant que le travail des forces de freinage se transforme intégralement en chaleur, déterminer la quantité de chaleur qui apparaît dans les freins d'un wagon sur une distance de freinage de 100 m.

Force de freinage ( supposée constante) sur un wagon de masse 10 t : F= 1900*10 = 1,9 104 N.

Travail résistant de cette force au cours d'un déplacement d =100 m :

W= -F d = -1,9 104 *10 = -1,9 106 J.

Les freins comportent sur chaque roue un dique d'acier de masse m=10 kg. La chaleur massique de l'acier est c= 500 J.kg-1.°C-1. Si les disques n'étaient pas refroidis, quelle serait l'élévation de la température de chacun de ces quatre disques d'un wagon au cours du freinage sur la distance de 100 m.

Q= m c Dq.

m = 40 kg : masse des 4 disques d'acier ; Dq : élévation de la température

Q = 1,9 106 J

Dq = Q/(mc) = 1,9 106 / (40*500) = 95 °C.

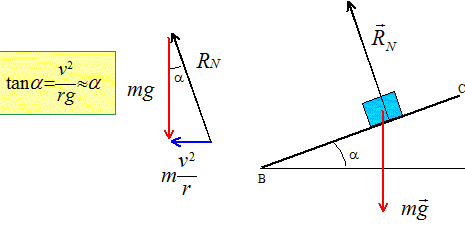
Le train parcourt une courbe horizontale, circulaire, à la vitesse constante v=30 m.s-1. Le rail extérieur est à un niveau supérieur par rapport au rail intérieur ; la dénivellation est h=12 cm. De ce fait la réaction des rails est perpendiculaire aux axes des roues. Ces dernières ne subissent pas d'efforts latéraux. On donne g=10m.s-2 ; écartement des rails : d=1,44 m. Soit a l'inclinaison du plan des rails par rapport à l'horizontale ; cet angle étant faible on peut utiliser l'approximation suivante tan a =sin a.

Faire un schéma et représenter les forces exercées sur le train au cours de cette nouvelle étape.

avec r : rayon de la courbe.

 

Donner l'expression du rayon r de la courbe décrite en fonction de g, h, d et v.

sin a = h/d voisin de tan a, voisin de a (radian)

d'où : h/d = v2/(rg) soit r = v2d/ (hg).

r = 302 *1,44 / (0,12*10) = 900*1,44 / 1,2 = 900*1,2 = 1080 m = 1,08 km.

 
 

 

retour -menu