|
On veut déterminer l'indice de réfraction n d'un prisme En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||
| .
. |
||||
|
||||
|
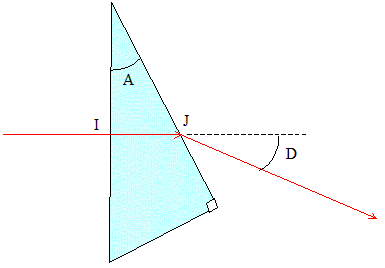
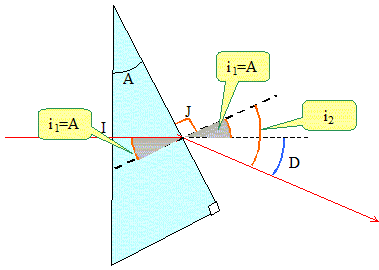
On envoie un rayon laser perpendiculairement à la surface d'entrée du prisme. Il ressort en ayant subit une déviation D par rapport à la direction initiale du rayon :
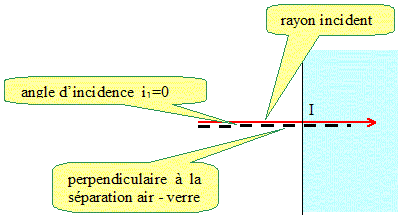
On donne A= 30 ° ; D= 30 ° et nair = 1,0. Pourquoi le rayon n'est-il pas dévié en I à la traversée de la surface de séparation entre l'air et le verre ?
La loi de Descartes concernant la réfraction s'écrit, en I : nair sin i1 = nverre sin i2. En I, l'angle d'incidence i1 est nul : sin i1 = 0. donc 0 = nverre sin i2 ; d'où sin i2 = 0 ou encore i2=0. Un rayon incident, perpendiculaire à la surface séparant deux milieux transparents, n'est pas dévié.
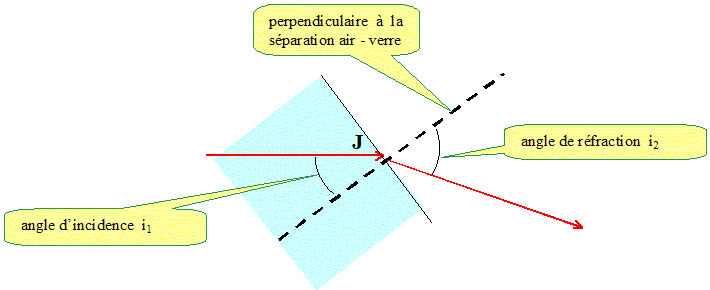
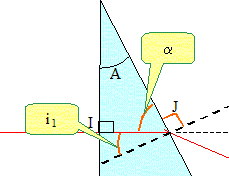
Placer sur le schéma l'angle d'incidence i1 et l'angle de réfraction i2 du rayon laser.
i1+a=90°
; A+a=90°
d'où
i1 = A =
30°. Exprimer i2 en fonction de A et de D :
i2 - i1 = D i2 -A = D ; i2 = D+A = 30 +30 = 60 °.
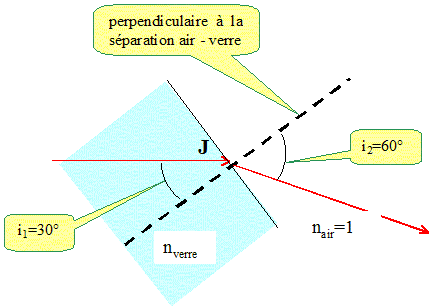
Ecrire la loi de Descartes en J concernant la réfraction. nverre sin i1 = nair sin i2. nverre = nair sin i2 / sin i1 nverre = 1* sin 60 / sin 30 = 0,866 / 0,5 nverre =1,7.
|
||||
|
|
||||
|
|