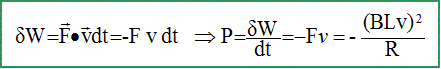|
freinage par induction concours général 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||||
| .
. |
||||||
|
||||||
|
Les vecteurs sont écrits en gras et en bleu.
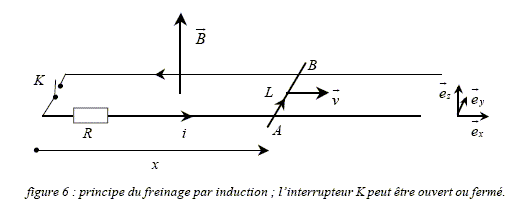
Le circuit est ouvert. On suppose dans un premier temps que l'interrupteur K est ouvert. Valeur de l'intensité i du courant dans le circuit : Si le circuit est ouvert, aucun courant électrique ne peut circuler et en conséquence i=0. Expression de la force électromagnétique F qui s'exerce sur la barre AB. La force de Laplace est proportionnelle à l'intensité du courant. L'intensité du courant étant nulle, alors la force électromagnétique est nulle : F=0. Quel sera alors le mouvement de la barre ? Le freinage est-il possible ? En absence de frottement la barre AB est pseudo-isolée. D'après le principe d'inertie, celle-ci est animée d'un mouvement rectiligne uniforme. Le freinage est impossible.
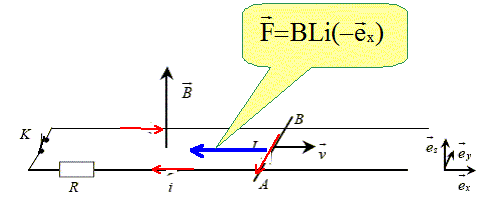
On ferme l'interrupteur K à la date t=0. On souhaite étudier la conséquence du phénomène d'induction électromagnétique dans le circuit. Montrons que la fem d'induction induite par le déplacement de la barre dans le champ magnétique vaut e=-BLv : La fem induite est donnée par la loi de Faraday : e = -dF / dt. où F =BS est le flux du champ magnétique B à travers la surface S du circuit. Expression de la surface S du circuit en fonction de l'abscisse x de la barre et de sa longueur L. S= x L. Expression de la fem induite e en fonction de B, L et v = dx/dt la vitesse de la barre. F =BS = BLx e = -dF / dt = -BL dx/dt ; e = -B l v. En déduire l'expression de l'intensité i du courant électrique dans le circuit. Quel est le signe de i ? e = R i ; i = e/ R ; i = -Blv/R Le signe moins indique que le courant a le sens contraire au sens choisi sur le schéma. On parlera de
freinage par
induction. Le module de F vaut : F= B2L2 v/R. Ce phénomène montre la réversibilité du moteur électrique. Fonctionnement en moteur : la barre AB, traversée par un courant, placée dans un champ magnétique est soumise à une force, sous l'action de laquelle elle se déplace. Le moteur est un récepteur électrique. Fonctionnement en générateur : la barre AB se déplaçant dans un champ magnétique génère un courant électrique dans le circuit. Bilan énergétique du freinage de la barre : Partant de sa vitesse initiale v0, la barre est freinée et fini donc par s'arrêter. On va effectuer un bilan d'énergie dans le circuit pour comprendre la nature du transfert énergétique qui permet le freinage. Déterminons le travail dW de la force électromagnétique F au cours du déplacement dx=vdt. En déduire la puissance mécanique correspondante P =dW /dt en fonction de R et i.
Or i = -Blv/R d'où P= -Ri2. Sous quelle forme l'énergie mécanique de la barre est-elle dissipée ? L'énergie mécanique de la barre est dissipée en énergie thermique ( effet Joule) dan le circuit résistif de résistance R. Quel dispositif pourraît-on mettre dans le circuit pour stocker cette énergie afin de la réutiliser dans les phases d'accélération du moteur ? Placer dans le circuit une batterie d'accumulateurs : ces derniers se chargent pendant les phases de freinage. Déterminons la variation DEm de l'énergie mécanique Em de la barre entre l'instant initial et l'instant final ( barre à l'arrêt ). La barre reste sur une horizontale : celle-ci est choisie comme origine de l'énergie potentielle de pesanteur. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. A t = 0, l'énergie mécanique est sous forme cinétique et vaut Em(0) = ½mv02. Lorsque la barre est à l'arrêt, l'énergie cinétique, et en conséquence l'énergie mécanique est nulle Em(fin) = 0 DEm= Em(fin) - Em(0) = -½mv02. L'énergie maximale récupérable vaut alors : ½mv02.
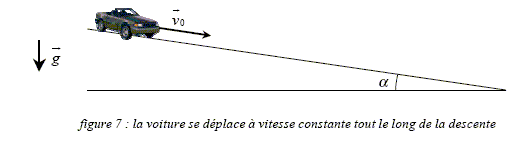
Freinage moteur en descente : Une voiture de masse m= 1000 kg, propulsée par un moteur électrique se déplace sur une route en pente descendante. Un panneau indique une pente de 10 % et qu'il faut utiliser le " frein moteur " de la voiture. Le conducteur qui connaît bien le fonctionnement du moteur électrique de sa voiture, remplace alors le système d'alimentation du moteur par un dispositif de stockage d'énergie électrique. Drâce au freinage par induction, la voiture conserve une vitesse constante v0 = 110 km/h tout le long de la descente.
On suppose valables toutes les
relations obtenues précédemment dans le cadre
du moteur linéaire.
Valeur de l'angle a ( radian) dont est inclinée la route par rapport à l'horizontale. sin
a = 10/100 = 0,1
;
a
= 0,1 rad.
Variation d'énergie cinétique dEc de la voiture pendant dt. La vitesse étant constante, l'énergie cinétique ne varie pas : dEc =0. Déterminons la variation d'altitude dh de la voiture au cours de ce déplacement dx. sin a = dh/dx, a étant petit sin a voisin a radian et dh = a dx. Variation d'énergie potentielle dEp de la voiture pendant dt. L'origine de l'énergie potentielle de pesanteur est prise en bas de la descente. Lors de la descente l'énergie potentielle diminue dEp = mg (-dh) = -mg a dx avec dx = v0 dt dEp = -mg a v0 dt. Variation dEm de l'énergie mécaniue de la voiture. dEm = dEc + dEp = 0 + ( -mg a v0 dt) Puissance mécanique réçue par la voiture. Pm = dEm/dt = -mg a v0 Interprétons le signe de la puissance. Le signe négatif traduit la conversion de l'énergie mécanique en énergie électrique.
On suppose que la variation d'énergie mécanique de la voiture est intégralement convertie en énergie électrique grâce au freinage par induction. Puissance électrique générée par le freinage par induction au cours de la descente : Pélec= mg a v0 v0 = 110 km/h = 110 / 3,6 = 30,56 m/s. Pélec= 1000 *9,81*0,1*30,56 = 3,0 104 W = 30 kW.
|
||||||
|
|
||||||
|
|