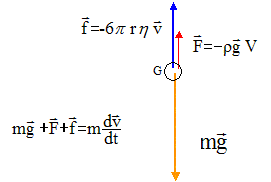|
Modélisation d'un écoulement autour d'une sphère : écoulement laminaire, écoulement turbulent concours général 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||
| .
. |
||||
|
||||
|
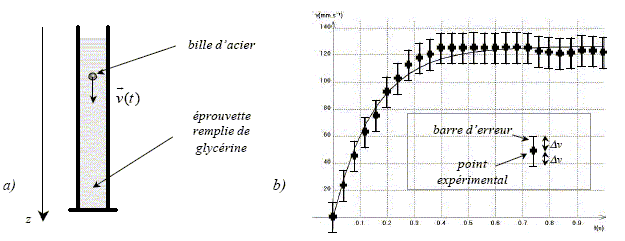
L'objectif est de comparer la chute de la bille dans la glycérine et dans l'eau. g = 9,81 m/s2. Chute de la bille dans la glycérine.
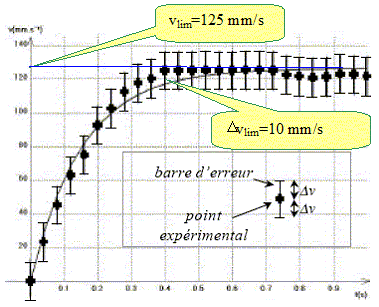
Masse volumique de la glycérine r = 1,26 103 kg m-3 ; viscosité h = 1,49 Pa s. La bille est lâchée sans vitesse initiale. L'évolution de la vitesse au cours du temps est donnée ci-dessus. A partir du graphe expérimental, décrire le mouvement de chute et mesurer la vitesse limite vlim : La vitesse augmente sur l'intervalle [0 ; 0,5 s] puis devient constante à t >0,5 s ( mouvement rectiligne uniforme )
On souhaite modéliser la force de frottement exercée par le fluide sur la bille par : f = -6p r h v ( les grandeurs écrites en gras et en bleu sont des vecteurs) Déterminer l'équation différentielle du mouvement de la bille. La bille est soumis à 3 forces: - la poussée d'Archimède, verticale, orientée vers le haut, valeur = poids du volume de fluide (air) déplacé : F= r V g avec r : masse volumique du fluide kg m-3 ; V : volume de la bille (m3) - le poids du système, verticale, orientée vers le bas, valeur : P= m g = rbille V g - la force de frottement de l''eau sur la bille, verticale, orientée vers le haut, valeur : f = 6p r h v ( négligeable au début du mouvement car la vitesse est alors très faible) Ecrire la seconde loi de Newton :
Sur un axe vertical descendant, cette loi s'écrit : rbille V g - 6p r h v- r V g = rbille V dv/dt. dv/dt + 6p r h / (rbille V) v = g(1-r /rbille) Donner l'expression de la vitesse limite vlim . Quand la vitesse limite est atteinte le mouvement est uniforme : dv/dt=0. 6p r h / (rbille V) vlim = g(1-r /rbille) vlim = g rbille V (1-r /rbille) / (6p r h).
V= 4/3pr3
= 4/3*3,14*(3,9 10-3)3 = 2,48
10-7 m3. 6p
r
h
= 6*3,14*3,9 10-3*1,49 =
0,109 vlim
=9,81*7,8 103 *2,48
10-7( 1-1,26/7,8) / 0,109 =0,146 m/s =
146
mm/s. Du même ordre de grandeur que la valeur
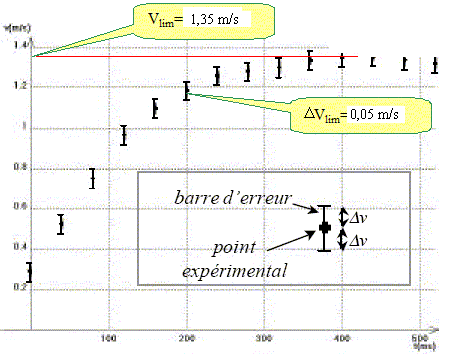
expérimentale. On reprend l'expérience précédente pour étudier la chute de la bille dans l'eau ( r = 1000 kg/m3 ; viscosité h = 1,0 10-3 Pa s). La bille est toujours lâchée sans vitesse initiale. A partir du graphe expérimental, décrire le mouvement de chute et mesurer la vitesse limite vlim : La vitesse augmente sur l'intervalle [0 ; 0,3 s] puis devient constante à t >0,3 s ( mouvement rectiligne uniforme )
Calculer la vitesse limite théorique. V= 4/3pr3 = 4/3*3,14*(3,9 10-3)3 = 2,48 10-7 m3. 6p r h = 6*3,14*3,9 10-3*10-3 = 7,35 10-5. vlim =9,81*7,8 103 *2,48 10-7( 1-1/7,8) / 7,35 10-5 = 225 m/s. En désaccord complet avec le modèle de la force de frottement fluide. Quelles sont les différences essentielles entre les deux expériences ? Les masses volumiques des deux liquides sont voisines. Par contre la viscosité de l'eau est environ 1500 fois plus faible que celle de la glycérine.
Ecoulement laminaire ; écoulement turbulent. La forme de l'écoulement d'un fluide autour de la bille dépend de la vitesse v et de la taille d de l'obstacle ( ici le diamètre de la bille), mais aussi de la masse volumique r et de la viscosité h du fluide considéré. Pour caractériser le régime d'écoulement on utilise le nombre sans dimension Re, appelé nombre de Reynolds défini par : Re = r v d /h. Parmi les différents régimes d'écoulement que l'on peut observer, on distingue en particulier : L'écoulement laminaire : Re <1 L'écoulement autour de l'obstacle est symétrique et régulier. La force de frottement fluide est donnée par la formule de Stokes : f = -6p r h v
L'écoulement turbulent :103<Re<105. L'écoulement est caractérisé par des variations spatio-temporelles importantes et aléatoire de la vitesse du fluide. La force de frottement s'exerçant sur la bille s'écrit : f = -½r CxS v2 u ( u : vecteur unitaire colinéaire à la vitesse et de même sens) Cx est le coefficient de traînée de l'obstacle dans le fluide : Cx = 0,43 pour un obstacle sphérique. S : surface frontale vue par le fluide: pour la bille étudiée : S= pr2.
Calculer le nombre de Reynolds correspondant aux expériences 1 et 2 lorsque la bille atteint sa vitesse limite. Re = r v d /h. Glycérine : 1,26 103 * 0,125 * 7,8 10-3 / 1,49 = 0,82. eau : 1,0103 * 1,35 * 7,8 10-3 / 10-3 = 1,1 104. Caractériser l'écoulement du fluide autour de la bille dans chaque cas. Dans la glycérine l'écoulemnt est laminaire. Dans l'eau l'écoulement est turbulent. Que dire du modèle utilisé pour l'expérience 1 ? Le modèle utilisé dans l'expérience 1 est valable. Exprimer la force de frottement qui s'exerce sur la bille plongée dans l'eau lorsqu'elle a atteint sa vitesse limite. f = -½r CxS v2 u Justifier la validité de cette expression. L'écoulement étant turbulent, la valeur de la force de frottement est : f =½r CxS v2 Déterminer alors l'expression de la vitesse limite de la bille. L'équation différentielle relative à la vitesse s'écrit : rbille V g - ½r CxS v2 - r V g = rbille V dv/dt. Lorsque la vitesse limite est atteinte, dv/dt = 0, d'où : ½r CxS v2 = V g(rbille - r ) v 2 =2V g(rbille - r ) / (r CxS) v 2 =2V g(rbille/r-1 ) / ( CxS) Or V= 4/3pr3 et S= p r2 ; V/S = 4/3r d'où : v 2 =8/3r g(rbille/r-1 ) / Cx. v = [8/3r g(rbille/r-1 ) / Cx]½. Calculer cette vitesse et conclure. v= [8/3*3,9 10-3 *9,81(7,8-1 ) / 0,43]½. v = 1,3 m/s. Du même ordre de grandeur que la valeur expérimentale. |
||||
|
|
||||
|
|