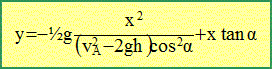théorème de l'énergie cinétique ; trajectoire d'une balle de golf concours Berck 98/99

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

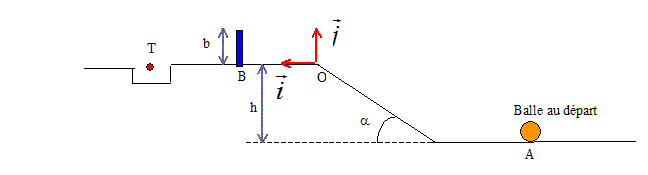
Le mini-golf de Berck fait la joie des petits et des grands. Un des points les plus difficiles à réaliser est représenté ci-dessous :

La balle , assimilée à un objet ponctuel de masse m, quitte le point A avec une vitesse horizontale v_A, monte la rampe d'angle a et de hauteur h, passe au dessus de la barrière de hauteur b et tombe dans le trou si "le point" est réussi.

Les résultats numériques seront exprimés avec trois chifres sinificatifs.

Les frottements avec le sol ou l'air sont négligés.

g = 10,0 m/s² ; a =30,0° ; h= 50,0 cm ; x_T= 3,00 m.

La barrière est au milieu des points O et T.

Donner une condition sur v_A, en fonction de g et h pour que la balle parvienne en O.

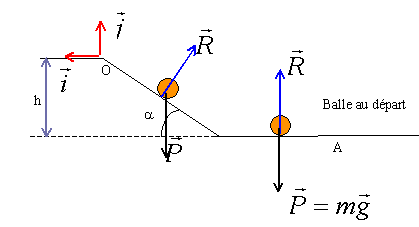
Ecrire le théorème de l'énergie cinétique entre A et O.

Sur le plan horizontal, les forces sont perpendiculaires à la vitesse : en conséquence elles e travaillent pas.

Sur la rampe seul le poids effectue un travail ( R, action du plan, est normale au plan).

le travail du poids est résistant en montée et vaut W= -mgh.

variation de l'énergie cinétique entre A et O :

DE_c = ½m v_O² - ½m v_A²

½m v_O² - ½m v_A² = -mgh

v_O² =v_A²-2gh.

Pour atteindre O avec une vitesse nulle, la vitesse minimale en A doit être : v_A = (2gh)^½.

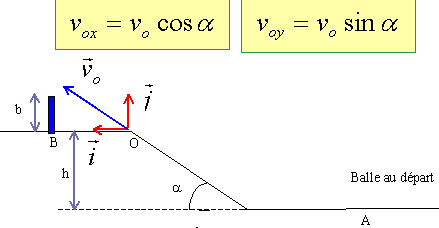
Déterminer les coordonnées du vecteur vitesse v_O, en O, en fonction de a, v_A, g et h. 

vox= (vA2-2gh)½cos a ; voy= (vA2-2gh)½sin a.

Au delà de O la balle est en chute libre ( elle n'est soumise qu'à son poids).

Composantes de l'accélération : ( 0 ; -g)

La vitesse est une primitive de l'accélération :

v_x = v_ox= (v_A²-2gh)^½cos a ; v_y = -gt + v_oy=-gt +(v_A²-2gh)^½sin a.

La position est une primitive de la vitesse :

x = v_x t = (v_A²-2gh)^½cos a t (1)

y = v_y t = -½gt²+(v_A²-2gh)^½sin a t (2)

(1) donne t = x / ( (v_A²-2gh)^½cos a)

repport dans (2) :

Calculer la valeur umérique de v_A pour que la balle parvienne en T, centre du trou.

abscisse de T : x_T=3 m ; ordonnée y_T=0 

0 = -0,5 g *3 / ((v_A²-2gh)cos²a) + sin a / cos a.

1,5 g / ((v_A²-2gh)cosa) = sin a ; 1,5 g = (v_A²-2gh)cosasin a

(v_A²-2gh) = 1,5 g / (cosasin a) ; v_A²=1,5 g / (cosasin a) +2gh

v_A²=15/(cos30 sin30) +2*10*0,5 =44,641

v_A= 6,68 m/s.

 x_B= 1,5 m ;

y_B=  -0,5*10*1,5² / ((6,68²-2*10*0,5) cos²30) + 1,5 tan 30

y_B= 0,433 m = 43,3 cm.

Donner l'encadrement nmérique de v_A ( en km/h) qui permet de réussir ce point.

ordonnée y_T=0 

0 = -0,5 g *x_T / ((v_A²-2gh)cos²a) + sin a / cos a.

0,5 g *x_T / ((v_A²-2gh)cosa) = sin a ; 0,5 g *x_T = (v_A²-2gh)cosasin a

(v_A²-2gh) = 0,5 g *x_T / (cosasin a) ; v_A²=0,5 g *x_T / (cosasin a) +2gh

 abscisse de T : x_T=2,9 m

v_A²=5*2,9/(cos30 sin30) +2*10*0,5

v_A= 6,59 m/s = 6,59*3,6 km/h = 23,7 km/h.

 abscisse de T : x_T=3,1 m

v_A²=5*3,1/(cos30 sin30) +2*10*0,5

v_A= 6,77 m/s = 6,77*3,6 km/h = 24,4 km/h.