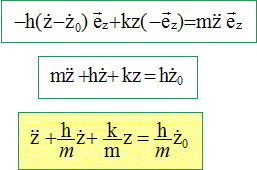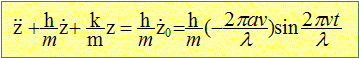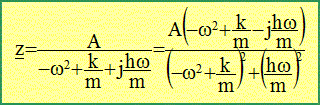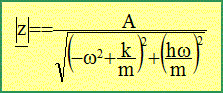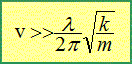amortisseur : oscillations mécaniques forcées concours ITPE ( travaux publics) interne 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

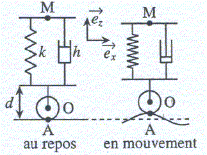
On rappelle qu'un amortisseur placé entre O et M exerce sur M une force de frottement fluide proportionnelle à la vitesse de M par rapport à O.

L'axe OM reste vertical.

On se propose d'étudier le comportement du véhicule lorsqu'il a la vitesse v suivant x sur une route dont le profil est défini par z_A(x) = a cos ( 2px/l).

La roue et la partie basse de la suspension sont supposés indéformables ( OA et d sont donc constantes).

Pour simplifier, on pourra supposer d=0. On note z_O(t) la variation d'altitude du point O par rapport à la position au repos. On repère le mouvement de la masse par son élongation z(t) par rapport à sa position d'équilibre stable quand le véhicule est au repos. On admet que le référentiel lié au sol est galiléen.

Que représente l dans l'expression de z_A(x) ?

z_A(x) = a cos ( 2px/l)

2p /l a la dimension de l'inverse d'une longueur.

l est une longueur " période spatiale" : distance séparant deux points consécutifs de la route se trouvant dans le même état.

Montrer que la force de frottement fluide peut s'écrire :

vitesse de M par rapport au sol = vitesse de M par rapport à O + vitesse de O par rapport au sol

V_{M / sol} = V_{M /O} + V_{O / sol}

V_{M /O} = V_{M / sol} - V_{O / sol}

"une force de frottement fluide proportionnelle à la vitesse de M par rapport à O"

d'où l'expression de f ci-dessus.

Etablir l'équation différentielle en z(t) du mouvement de la masse lorsque la vitesse v suivant x est constante . M est soumise à une force de rappel due au ressort et à la force de frottement fluide. Ecrire la seconde loi de Newton suivant z.

La vitesse v étant constante suivant x : x= vt

z_A(t) =z_O(t) = a cos ( 2pvt/l)

z'_O = -2pav/l sin( 2pvt/l)

Déterminer l'amplitude du mouvement d'oscillation vertical du véhicule en régime permanent.

On pourra utiliser la notation complexe z =Z exp(jwt), calculer l'amplitude complexe Z et en déduire l'amplitude réelle correspondante.

La route joue le rôle d'excitateur : elle impose sa fréquence.

z' =Zjw exp(jwt)= jwz

z" =-Zw² exp(jwt) = -w²z

-2phav / (ml) =A ; 2p/ l= w ; A sin (wt)

Grandeur complexe associée : A exp(jwt)

L'équation différentielle s'écrit :

-w²z + h/m jw z + k/m z = A exp(jwWt)

[-w²+ k/m +j h/m w ] z = A exp(jwt)

amplitude complexe :

amplitude réelle : module du nombre complexe z.

 A quelle allure convient-il de rouler pour que cette amplitude soit aussi faible que possible ?

Le dénominateur de l'expression ci-dessus doit être le plus grand possible.

C'est à dire w² >>k/m.

On doit se trouver le plus loin possible de condition de résonance ( w² =k/m)

Or z_A(x) = a cos ( 2pvt/l) soit w =2pv/l

(2pv/l)² >>k/m