|
moteur à deux temps ; vaporisation de l'eau concours ITPE ( travaux publics) interne 2006 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||
| .
. |
||||
|
||||
|
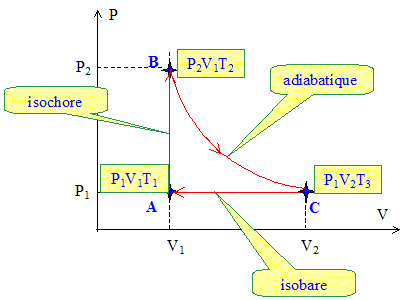
- L'air et le carburant sont admis dans le cylindre ; à la fin de la phase d'admission, l'air se trouve dans l'état A( P1, V1, T1) - La combustion du carburant ( phase d'explosion) provoque une augmentation brutale de la pression à volume constant et fournit un transfert thermique Q1. A la fin de cette phase, les gaz résiduels sont dans un état B(P2, V1, T2). - Ils se détendent ensuite de manière adiabatique jusqu'à l'état C( P1, V2, T3) - Enfin les gaz s'échappent du cylindre à pression constante P1 et un nouveau cycle commence. On néglige la quantité de matière de carburant liquide, on assimile l'air et les gaz brûlés à des gaz parfaits dont le coefficient g=cP/cV=1,4 et on suppose que le cycle est constitué de transformations réversibles. Représenter dans le diagramme PV, le cycle de transformation ABCA des gaz ( air ou gaz brûlés) dans le cylindre.
Calculer le travail échangé par n moles de gaz au cours d'un cycle en fonction de R, g, T1, T2, T3. A--> B isochore dW=-PdV ; W=0. B--> C adiabatique Pas d'échange de chaleur avec l'extérieur ; DU= W+Q =W+0 = W W= n cV (T3-T2) vec cV= R/(g-1) W= nR/(g-1)(T3-T2). C--> A isobare dW=-PdV ; W= -P1(V1-V2) = -P1V1+P1V2 Or P1V1 = nRT1 et P1V2 = nRT3 W= nR(T3-T1 ). W= nR[ (T3-T2 )/(g-1)+T3-T1 ] = nR/(g-1) [(T3-T1 )g+T1-T2]
Le rendement est défini par r = -W/Q1. A---> B :
DU=
W+Q1 =0+Q1
=Q1 =
ncV(T2-T1) Q1
=
nR/(g-1)(T2-T1) r = -W/Q1
=
[(T3-T1
)g+T1-T2]
/ (T1-T2) r =
g
(T3-T1
)/ (T1-T2)
+1. T1 = P1V1/(nR) ; T2= P2V1/(nR) ; T3 = P1V2/(nR) ; T3 -T1 =P1/(nR) (V2-V1) ; T1 -T2 =V1(P1-P2) /(nR). r = g P1 (V2-V1) / [ V1(P1-P2 ]+1 r = g P1 /(P1-P2) (a-1)+1 r = g (a-1) / [1-P2/P1] +1 Or la transformation B--> C est une adiabatique réversible, d'où P2V1g = P1V2g . P2/P1= V2g / V1g = ag r = g (a-1) / [1-ag] +1. Calculer r pour a=4. r= 1,4*3/(1-41,4) +1 = 0,30.
On place une ampoule contenant m= 0,01 kg d'eau liquide dans une enceinte indéformable de volume V maintenue au contact d'un thermostat à la température T0=373 K. Initialement l'enceinte est vide et l'eau dans l'ampoule est à la température T0 et sous une pression initiale égale à la pression de vapeur saturante Ps(T0)=1 bar. La vapeur d'eau est assimilée à un gaz parfait de masse molaire M=18 g/mol. On donne l'enthalpie massique de vaporisation de l'eau Lv(T0) = 2,3 103 kJ kg-1 et on néglige le volume massique de l'eau liquide devant celui de la vapeur d'eau. Calculer la valeur particulière VC du volume V pour que l'eau dans l'état d'équilibre final soit à la température T0 sous la pression Ps(T0)=1 bar avec un titre en vapeur xV=1. Le liquide est entièrement vaporisé. Ps(T0) VC = nRT0. Ps(T0) = 105Pa ; T0 = 373 K ; R= 8,31 J mol-1 K-1 ; n = m/M = 10/18 = 0,555 mol VC = nRT0 / Ps(T0) = 0,555 *8,31*373 / 105 = 1,72 10-2 m3 = 17,2 L. Calculer pour l'évolution correspondante le transfert thermique Q reçu par l'eau. Q = m Lv(T0) =0,01* 2,3 103 = 23 kJ. Calculer la variation d'entropie de l'eau, l'entropie échangée, l'entropie créée et commenter. DS= Q /T0 =23000 / 373 = 61,7 J K-1. variation d'entropie = entropie échangée entre le fluide et le milieu extérieur + entropie produite lors de la transformation au sein du fluide L'entropie échangée est nulle. La variation d'entropie est égale à l'entropie créée : l'entropie est positive car on passe d'un milieu condensé à un gaz, milieu plus désordonné.
On suppose que le volume V est inférieur à VC. Déterminer l'état d'équilibre final. Une partie de l'eau se vaporise. quantité (mol) d'eau vaporisée : n= Ps(T0) V/(RT) On suppose que le volume V est supérieur à VC. Déterminer l'état d'équilibre final. Toute l'eau est vaporisée. La pression finale vaut : P= nRT/ V, valeur inférieure à Ps(T0). |
||||
|
|
||||
|
|