Aurélie 13/10/07
 

Bobine inductive concours ITPE ( travaux publics) interne 2004

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

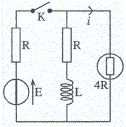
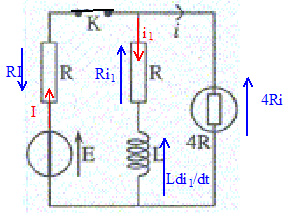
La résistance de la lampe est 4R.

Avant que l'on ne ferme l'interrupteur K, le circuit est"abandonné" pendant suffisamment longtemps pour que le régime permanent soit atteint. A t=0, on ferme K.

Décrire l'état du circuit à t=0-, juste avant la fermeture de K.

L'intensité est nulle dans tous les dipoles.

La tension aux bornes de l'interrupteur K est égale à la tension E aux bornes du générateur.

Déterminer l'intensité i(0+) qui circule dans la lampe juste après la fermeture de K.
La branche contenant la bobine d'inductance L n'est traversée par aucun courant . Cette bobine introduit un retard à l'établissement du courant dans cette branche.

Le générateur est en série avec un conducteur ohmique de résistance 5 R.

L'intensité qui traverse la lampe vaut i(0+) = E/(5R).

Calculer l'intensité du courant i(t) dans la lampe pendant le régime transitoire ( t>0)

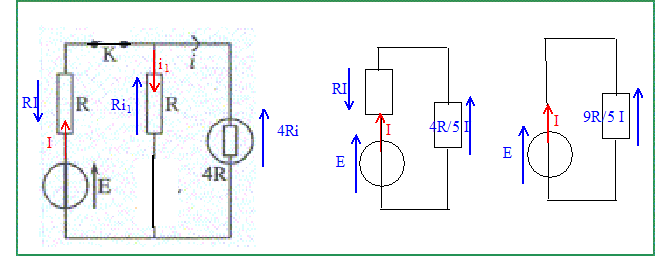
Loi des noeuds : I = i + i1.

additivité des tensions : E-RI = 4Ri = Ri1 + Ldi1/dt.

or i1 = I-i d'où di1/dt = dI/dt -di/dt.

E-RI = 4Ri donne dI/dt = -4di/dt

par suite di1/dt = -5Ldi/dt.

4Ri = Ri1 + Ldi1/dt s'écrit : 4Ri =R(I-i) -5Ldi/dt.

E-RI = 4Ri donne I= E/R-4 i d'où : 4Ri =R(E/R-5i) -5Ldi/dt.

9R i +5Ldi/dt = E ; di/dt + 9R/(5L) i = E/(5L). (1)

On pose t = L/(4R)

solution générale de cette équation sans second membre : i = A exp(-t/t)

solution particulière de (1) : i = E/(9R)

solution générale de (1) : i = E/(9R) + A exp(-t/t)

à t=0+, i = E/(5R) d'où E/(5R) =E/(9R) + A ; A= 4E/(45R)

i = E/(9R) + 4E/(45R) exp(-t/t)

i = E/(9R) ( 1+ 4/5exp(-t/t) ).

 
En déduire l'intensité du courant dans la lampe lorsque le nouveau régime permanent est atteint.

exp(-t/t) tend vers zéro au bout de t = 5 t

i = E/(9R)

Autre méthode.

En régime permanent le terme Ldi1/dt est nul et le circuit est équivalent à :

Une fois ce nouveau régime permanent atteint, on ouvre à nouveau K. On prendra cet instant de réouverture de l'interrupteur comme nouvelle origine des temps t=0.

Calculer i(t) en prenant soin de définir la condition initiale i(0+).

i(0+) = E/(9R).

 

 

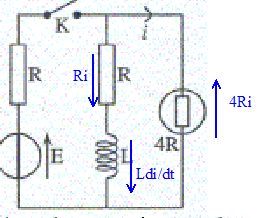
Ri + Ldi/dt + 4Ri = 0

di/dt + 5R/L i = 0 ; on pose t1 = L/(5R)

i = B exp(-t/ t1)

Or i(0+) = E/(9R) d'où B = E/(9R)

i(t) = E/(9R)  exp(-t/ t1).

Sachant que la lampe ne s'allume que pour i > E/(8R), quel peut bien être son rôle ?

L'intensité i n'atteint jamais la valeur E/(8R) : la lampe ne s'allume pas.

La dissipation de l'énergie électromagnétique stockée dans la bobine inductive à travers la lampe sous forme de chaleur ( effet Joule) évite une étincelle de rupture aux bornes de l'interrupteur lors de l'ouverture de celui-ci.


 

retour -menu