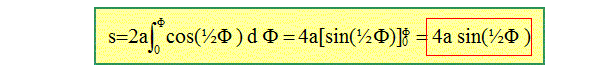|
Mécanique : anneau sur un morceau de cycloïde concours ITPE ( travaux publics) interne 2004 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||
| .
. |
|||||
|
|||||
|
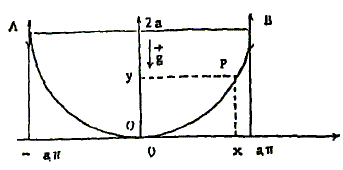
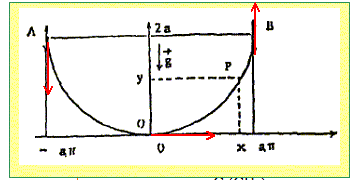
Dans ce plan, un fil de fer, de section négligeable, a la forme d'un morceau de cycloïde défini par ses équations paramétriques x= a(F+sin F ) ; y = a(1-cosF). a constante positive ; F est compris entre -p et +p.
Donner en fonction de F les différentielles dx et dy. dx= a(1+cos F) d F ; dy = a sin F dF. En déduire celle de la pente y'(F) du graphe et vérifier que les tangentes qui y sont représentées ont bien l'allure convenable y'(+ ou - p) et y'(0). y' = dy/dx = sin F / (1+cos F) . or sin F = 2 sin (½F) cos (½F) et 1+ cos F = 2 cos2(½F) d'où y' = tan(½F) y'(0) = 0 = tangente horizontale y'(-p) tend vers - l'infini : tangente verticale ; y'(+p) tend vers + l'infini : tangente verticale.
On abandonne en A, sans vitesse initiale, un anneau de taille négligeable et de masse m qui glisse sans frottement sur le fil de fer. Donner l'expression de la différentielle de l'abscisse curviligne s=OP de cet anneau, quand celui-ci se trouve au point P(x,y). On rappelle que (ds)2 = (dx)2 + (dy)2. (dx)2= a2(1+cos F)2 (d F)2 = a2[1+2cos F+ cos2F] (d F)2 (dy)2 = a2 sin2 F (d F)2 (ds)2 = a2 [1+2cos F+ cos2F+ sin2 F ] (d F)2 (ds)2 = a2 [1+2cos F+ 1 ] (d F)2 (ds)2 = 2a2 [1+cos F ] (d F)2 = 4a2 cos2(½F)(d F)2 ds = 2a cos(½F) d F .
Toujours pour cet anneau en P, trouver en fonction de F l'expression de : L'énergie potentielle Ep , l'origine étant prise en O(0 ; 0). Ep= mg y = mg a (1-cosF) Or 1-cosF = 2 sin2(½F) d'où Ep= 2mga sin2(½F). Ep(0) = 0 ; Ep(p) =Ep(-p) = 2mga. L'énergie cinétique Ec. Ec= ½mv2 = ½m ( ds/dt)2 avec ds/dt = ds/dF *dF/dt = ds/dF F'. Ec= ½m [2a cos(½F)]2F'2 = 2a2 m cos2(½F)]2F'2 L'énergie cinétique est nulle en A ( pas de vitesse initiale) ; en conséquence elle est nulle en B. L'énergie mécanique est constante ( absence de frottement) et vaut 2mga en O, l'énergie mécanique est sous forme cinétique et vaut : Ec(0) = 2mga.
EM= Ep+Ec = 2mga sin2(½F) + 2a2 m cos2(½F)]2F'2
On pose q= sin(½F). Exprimer l'énergie mécanique en fonction de q et q'=dq/dt. q' = ½ cos(½F) F'. EM=2mga q2 + 8a2 m q'2 = 2 ma ( g q2 + 4aq'2 ). Montrer qu'une différentiation supplémentaire, par rapport au temps, de EM conduit à une équation différentielle du type : q" + w2q = 0 . Préciser la valeur de w. EM/ (2am) = g q2 + 4aq'2 = constante différentier par rapport au temps : 0 = 2gq q' +8aq' q" gq + 4a q"=0 soit q" + g/(4a) q=0 avec w=[g/(4a)]½. En déduire la loi horaire q(t). A t=0, l'anneau passe pour la première fois en O(0;0). La solution de l'équation différentielle ci-dessus est du type q= A sin (wt+j) Or à t=0, y=0 soit F= 0 ; q=0. A sin j = 0 conduit à j = 0 et q= A sin (wt) Comment trouver A ? q'(0) = Aw En O l'énergie mécanique st sous forme cinétique et vaut : 2mga =8a2 m q'2 soit q'= [g/(4a)]½. par suite : [g/(4a)]½ = Aw ; A= [g/(4a)]½ / w ; A= [g/(4a)]½ [g/(4a)]-½ =1 q=sin (wt) Donner l'expression de s(t) : s(t) = 4a sin (½F) = 4a sin (wt).
|
|||||
|
|
|||||
|
|