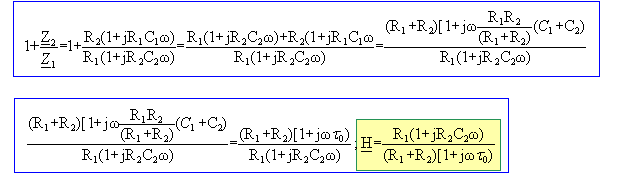Aurélie 25/09/07
 

Nombres complexe en électricité concours ITPE ( travaux publics) interne 2004

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

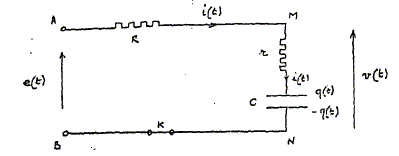
Pour étudier les phénomènes en régime permanent il est conseillé d'utiliser la notation complexe en représentant une grandeur sinusoïdale s(t) = 2½ S cos (wt+F) par la grandeur complexe s= S 2½ exp(jF) avec S l'amplitude complexe de la grandeur considérée.

On réalise le circuit ci-dessous. e(t) = 2½ E cos (wt)

Donner l'expression de l'impédance complexe de ce circuit : on posera t =(R+r)C et t'=rC.

réponse :

Les dipôles sont en série : les impédances complexes de chaque dipôle s'ajoutent

z = R+r-j/(Cw) = [(R+r) Cw -j] / (Cw) = (tw--j )/ (Cw).

Donner les expressions des amplitudes complexes I, Q, V de i(t), q(t) et v(t) en fonction de E.

 

réponse :

i(t) = e(t) / z ; I = e / z avec e = E 2½

I = E 2½ Cw / [ tw -j]

Multiplier numérateur et dénominateur par l'expression conjuguée : [ t w+j]

I = E 2½ Cw / [ (t w)2+1] [ t w+j ].

La charge q(t) est une primitive de l'intensité i(t). Intégrer c'est diviser par jw, d'où :

Q = I / (jw) = E 2½ C / [ (t w)2+1] [ 1-jt w ].

v(t) = q(t) / C + r i(t) = 1/C [ q(t) + rC i(t)] = 1/C [ q(t) + t' i(t)]

V = 1/C [Q+ t' I ] = E 2½ / [ (t w)2+1] [ 1-jt w] + t' E 2½ w /[ (t w)2+1] [ t w+j].

V =E 2½ /[ (t w)2+1] [1-jt w+t'w( t w+j) ]

V =E 2½ /[ (t w)2+1] [1+t' t w2+j w(t'-t) ].

La tension de sortie est de la forme v(t) = V2½ cos (wt+F).

Calculer V et F ?

R= 40 kW ; r= 30 kW ; C= 0,1 mF ; w=314 rad/s et E= 220 V.

 réponse :
Module de V :

V =E 2½ /[ (t w)2+1] [(1+t' t w2)2+ (w(t'-t))2 ]½.

argument F de V :

tan F = w(t'-t) / (1+t' t w2)

t = 7 104 * 10-7 = 7 10-3 s ; t' = 3 104 * 10-7 = 3 10-3 s

(t w)2+1 = (7 10-3*314)2 +1 = 5,83 ; ( 1+(t' t w2)2 = ( 1+2,1 10-5 *3142)2 =9,43.

(w(t'-t))2 =3142(3-7)2 10-6 =1,58 ; [(1+t' t w2)2+ w2(t'2+t2) ]½ = (9,43+1,58)½ =3,32.

V = 220*1,41 /5,83 * 3,32 ; V = 176,5 V.

w(t'-t) = 314(3-7) 10-3 = -1,256 ; 1+t' t w2 = 1+2,1 10-5 *3142 = 3,07.

tan F = -1,256/3,07 = -0,607 ; F = -22,2°.
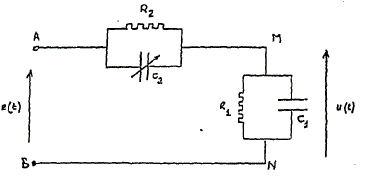
On considère le circuit suivant avec u(t) = 2½ U cos (wt+Y).

On pose R0 = R1R2 / (R1+R2) ; t1=R1C1 ; t2=R2C2 ; t0=R0(C1+C2 ). R1= 1 MW et R2= 9 MW

Montrer que la fonction de transfert complexe peut se mettre sous la forme :

H= 1/K [1+jwt2] / [1+jwt0]

H= U / E avec U = U 2½exp(-jY)

Impédance complexe de la branche AM :

Condensateur et résistance sont en dérivation, calculer l'admitance, inverse de l'impédance.

admittance complexe Y2 = 1/R2 + jC2w = 1/R2 (1+ jR2C2w) = 1/R2 (1+ jt2w)

impédance correspondante : Z2 =R2 /(1+ jt2w)

Impédance complexe de la branche MN :

admittance complexe Y1 = 1/R1 + jC1w = 1/R1 (1+ jR1C1w) = 1/R1 (1+ jt1w)

impédance correspondante : Z1 =R1/(1+ jt1w)

U = Z1 I ; E = (Z1 +Z2) I

H= U / E = Z1 / (Z1 +Z2) = 1/ [1+Z2/Z1 ]

Z2/Z1 = R2/R1 (1+ jt1w) / (1+ jt2w)

 



Expression de K :

H= 1/K [1+jwt2] / [1+jwt0]

On identifie K à : (R1+R2)/R1 :

K= 10.
retour -menu