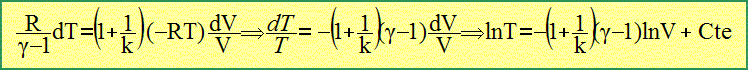|
thermodynamique : gaz parfait ; thermomètre à gaz concours ITPE ( travaux publics) interne 2003 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||
| .
. |
||||
|
||||
|
Déterminer en fonction de k et de g la constante n telle que TVn-1= Cte. La variation de l'énergie interne est égal à la somme du travail (-PdV) et de la chaleur dQ échangés entre le système et l'extérieur. dU= d W+dQ = (1 + 1/k) (-PdV) La variation de l'énergie interne d'un gaz parfait ne dépend que de la température. d U= CV dT avec CV capacité thermique molaire à volume constant. De plus CV = R / (g-1) d'où : R / (g-1)dT = (1+1/k)(-PdV) L'équation des gaz parfaits donne : P= RT/V
On pose n-1 = (1+1/k) (g-1). ln T = ln V1-n + Cte ; ln T - ln V1-n = Cte ; ln T + ln Vn-1 = Cte.
Calculer k si n=1,1 et g=1,2. n-1 = (1+1/k) (g-1). 1,1-1 = (1+1/k) ( 1,2-1) 1+1/k = 0,5 ; k = -2. A l'état initial la pression est P= 4 bars et la température T=300 K. A l'état final, le volume est V' = 9 L. Calculer T'. V= RT/P = 8,32 * 300/4 105 = 6,24 10-3 m3 = 6,24 L. T Vn-1 = T ' V ' n-1 ; T ' = T (V/V')n-1 ; T' = 300 (6,24/9)0,1 =2,89 102 K. P' = RT ' / V' = 8,32 *289 / 9
10-3 P' = 2,67 105 Pa =
2,67
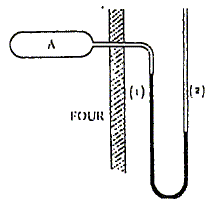
bar. Thermomètre à gaz. Un thermomètre à gaz se compose d'une ampoule A de volume invariable V= 2 L, contenant du dihydrogène, et communiquant avec un tube en U. Le diamètre intérieur du tube est très petit, et l'on admet que les variations de niveau du mercure ne modifient pas le volume du gaz enfermé dans l'appareil. L'ampoule A est enfermée à l'intérirur d'un four.
Lorsque le four est froid, c'est à dire à la température du laboratoire t1=20°C, le niveau du mercure dans la branche 1 est à la hauteur h1=50 cm au dessus du niveau du mercure dans la branche 2. On donne pour le mercure r g= 13,6 104 SI ; Patm = 1 bar. Quelle est la pression de l'hydrogène dans A à la température t1 ? Le gaz dans l'ampoule est en dépression. La différence de pression par rapport au laboratopire vaut : DP= r g h1 DP= 13,6 104 *0,5 = 6,8 104 Pa Pression de H2 dans l'ampoule : P1= 105 - 6,8 104 =3,2 104 Pa. Quelle doit être la température du four pour que le niveau du mercure soit le même dans les deux tubes ? La pression de H2 dans A vaut P2=105 Pa. P2 V = nRT2 ; P1 V = nRT1 ; T2=P2T1 / P1. T2 =105 *293 / 3,2 104 = 916 K. (643 °C)
Les dimensions du tube sont telles que le niveau du mercure dans la branche 2 peut être supérieure de hm = 50 cm à celui du mercure dans la branche 1. Quelle est alors la température du four ? Le gaz dans l'ampoule est en surpression. DP= 13,6 104 *0,5 = 6,8 104 Pa Pression de H2 dans l'ampoule : P3= 105 + 6,8 104 =1,68 105 Pa. T3=P3T1 / P1. T3 =1,68105 *293 / 3,2
104 = 1538
K. (1265 °C)
On désigne par x la dénivellation du mercure entre les deux branches, cette grandeur étant positive lorsque le mercure est plus haut dans la branche2 et négative lorsque le mercure est plus haut dans la branche 1. La hauteur x varie dans l'intervalle [-0,5 m ; 0,5 m] Etablir la relation t=f(x) donnant la température du four en fonction de la dénivellation mesurée. Pression du gaz dans l'ampoule : P = 105 + r g x = 105 + 13,6 104 x P = P1/T1 T = 3,2 104 / 293 T = 109,2 T T= 273 + t avec t en °C et T en K. d'où : 109,2 (273+t) = 105 + 13,6 104 x 273+t = 105 / 109,2 + 13,6 104 / 109,2x 273+t = 916 + 1245 x t = 643 +1245 x.
|
||||
|
|
||||
|
|